Math Basics Math Menus Functions Variables Built-in Math Animation
Graph Basics Plot Markup Graph Slicing
QM Waves Eigen-Energies Scattering QM Statistics QM Math
QMTools supports the computation of quantum probabilities, expectation values, and uncertainties. These state-specific operations are carried out by referencing an appropriate quantum wavefunction assigned on the Math Palette.

Probabilities
- On the Math Palette, enter the cumulative weight function: type
"wts" followed by (in parentheses) the reference wavefunction,
and values for the lower and upper bounds of the interval for the calculation.
The built-in function wts(ψ(..), a, b) accumulates the
statistical weights over the interval [a, b], and
ψ(..) furnishes those weights as |ψ(..)|2.
 To be properly recognized, the weighting function argument must be
"(..)" (two periods surrounded by parentheses).
To be properly recognized, the weighting function argument must be
"(..)" (two periods surrounded by parentheses).
- Type ctrl+Z to evaluate the expression. The
probability over the designated range is written to the right of the equality.
If a problem is encountered during evaluation, an error mark and accompanying
message appear in place of the computed value.
 To be interpreted as a probability, the weights accumulated over the
entire range of the independent variable must sum to unity, i.e., the
wavefunction furnishing those weights must be normalized.
To be interpreted as a probability, the weights accumulated over the
entire range of the independent variable must sum to unity, i.e., the
wavefunction furnishing those weights must be normalized.

Expectation (Average) Values & Uncertainties
- On the Math Palette, assign the expression to be averaged to a function, following the procedure outlined in Functions. To obtain reliable results, the independent variable must match the argument of the weighting function that supplies the statistics.
- Again on the Math Palette, enter the average function: type "avg"
followed by (in parentheses) the name of the function to be averaged (along
with its argument), and then the wavefunction furnishing the statistics, e.g.,
avg(f(x), ψ(..)).
 Unlike probabilities, the wavefunction furnishing statistical
weights for the calculation of averages need not be normalized.
Unlike probabilities, the wavefunction furnishing statistical
weights for the calculation of averages need not be normalized.
- Type ctrl+Z to evaluate the expression. The function average is written to the right of the equality. If a problem is encountered during evaluation, an error mark and accompanying message appear in place of the function average.
- Standard deviations are evaluated similarly, but with the standard deviation function "std" replacing "avg" in the above procedure. The uncertainty associated with any observable in a given quantum state is the standard deviation of the observable calculated from probabilities furnished by the wavefunction describing that state.
 Both "avg" and "std" are built-in operations that take
an expression with one independent variable as the first argument and a weighting
function as the second argument. The expression to be averaged can be defined as
a separate function (as above), or entered directly as an argument to the
statistical functions.
Both "avg" and "std" are built-in operations that take
an expression with one independent variable as the first argument and a weighting
function as the second argument. The expression to be averaged can be defined as
a separate function (as above), or entered directly as an argument to the
statistical functions.
To calculate the average of x3 using statistical weights furnished by the wavefunction ψ(x), we need add just a single entry to the Math Palette: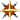 Example:avg(x3, ψ(..))Again, ψ(x) need not be normalized.
Example:avg(x3, ψ(..))Again, ψ(x) need not be normalized.
Momentum-Space Waves & StatisticsQuantum states can be expressed in many ways, the Schrödinger wavefunction ψ(x) being just one; the momentum-space wavefunction is another. The latter is useful for computing statistics of momentum-based observables.
The momentum-space and Schrödinger wavefunctions are fourier transforms of one another. QMTools uses the built-in fourier transform function "fft" to relate them.
- On the Math Palette, define the momentum-space wave, say φ(k), and
assign to it the expression fft(ψ(..), k). Here "ψ" is the
name of the Schrödinger wavefunction and "k" denotes the transform
variable.
 Unless previously specified, the domain of the transform variable "k"
defaults to a symmetric interval centered at the origin. The domain properties can
be changed from the Domain Editor (right-click anywhere within the formula field, and select
Set Domain... from the popup menu).
Unless previously specified, the domain of the transform variable "k"
defaults to a symmetric interval centered at the origin. The domain properties can
be changed from the Domain Editor (right-click anywhere within the formula field, and select
Set Domain... from the popup menu).
- Just like its Schrödinger counterpart, the momentum-space wave furnishes statistical
weights used to calculate probabilities and averages for momentum-based observables.
To calculate the average momentum and momentum uncertainty for a state described by the Schrödinger wavefunction ψ(x), we would add the following entries to the Math Palette: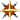 Example:φ(k) ≡ fft(ψ(..), k)Following each of the last two entries, type ctrl+Z to obtain the result.
Example:φ(k) ≡ fft(ψ(..), k)Following each of the last two entries, type ctrl+Z to obtain the result.
avg(k, φ(..))
std(k, φ(..)) - Since kinetic energy is a function of momentum, average kinetic energy can be found using the momentum space wave to furnish statistical weights. A convenient alternative uses the built-in average kinetic energy function "avgK" to calculate this important quantity directly from any Schrödinger wave ψ(x) and particle mass m as KE = avgK(ψ(..), m).