Last updated: March, 2018.
QMTools Help:  Functions

From the Math Palette, you may define functions of any number of variables, and the function may return a real or complex number.

Mouse and keyboard input is described below for the Windows platform; for Mac users, a right-click becomes a ctrl-click, and cmd substitutes for ctrl in all keyboard shortcuts.

divider
Creating a Custom Function

  1. Click the left mouse button in an area of the Math Palette where the first character will be placed, then type the function name followed by the argument list. The argument list contains all the independent variable names, separated by commas and enclosed in parentheses. For instance, you would type f(a,b,c) to specify a function named "f" defined for the three variables a, b, and c. Names are case sensitive, and may contain digits but must start with a letter.
    Function and variable identifiers may take subscripts. Subscripts are limited to alphanumeric characters (but function subscripts are numerical-only). Subscripts are not formula-based, so they may not include any arithmetic operations (not even a leading minus sign).

    To subscript a variable, type the variable name followed by ctrl+J.

  2. Next, type ctrl+X; this inserts the symbol "≡" and is the signal that you are defining something.
  3. Now enter the formula that will be used to calculate the function value, then type ctrl+Z. This last action tells the math engine to associate the formula with the function name, a process known as registering. When the engine successfully registers a function, it prints another equal sign followed by a checkmark. Failure to register properly causes an error mark to be printed, along with some explanation of the problem encountered.
  4. A successfully-registered function is evaluated by typing its name followed by a list of values for the independent variables, followed by ctrl+Z.
    QMTools recognizes a special notation for functions of a single variable that facilitates their use as arguments to other functions: f(..) specifies that the function "f" is to be evaluated over the entire domain of its argument (for examples of this usage, see Built-in Math).

Back to Top

divider
Complex-valued Functions

A complex-valued function returns a complex number as the result of an evaluation of real arguments. Such functions may be defined as separate real and imaginary parts [rectangular form]; the imaginary part is distinguished as the multiplier of the imaginary unit, which can be inserted on the Math Palette using the keyboard shortcut alt+ctrl+I. Polar forms also may be used if desired.

Evaluation of a complex function produces an ordered pair of real numbers, one each for the real and imaginary part, i.e., the result of evaluation is always reported in rectangular form.

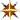Example:

The complex function f(x) with real part 2x and imaginary part 3 + x3 would be entered as shown below; the result of evaluating the function at x = 3 is also shown.
f(x) ≡ 2⋅x + (3 + x3)î
f(3) = (6, 30)

Back to Top

divider
The Algebra of Functions

Functions may be added, subtracted, multiplied and divided to create other functions, as illustrated below.

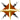Examples:

f(a) ≡ a2
g(b) ≡ 3⋅b − 1
h(a) ≡ f(a) + g(a)
h(2) = 9.0
j(b) ≡ f(b)⋅g(b)
j(1) = 2.0

k(x) ≡ sin(x) + f(2⋅x)
k(1) = 4.841470984807897

Back to Top