Within its limitations, QMTools furnishes the mathematical infrastructure for exploring the quantum world. That exploration starts with the quantum state, characterized by a wave function that encapsulates all things knowable about a given system. Wave functions come in two varieties – stationary and non-stationary – a reference to their evolution over time. QMTools deals with both.

Mass and Potential Energy

Before any quantum wave can be created, the particle mass and potential energy must be specified, in appropriate units. These entries are made on the Math Palette.

1. Begin by adjusting applet units to comply with any numerical values you expect to enter for mass and potential energy. Unit selection is explained fully under the heading Applet Basics.
2. Enter the desired mass on the Math Palette by typing a name for this variable, followed by ctrl+X, followed by a value. Validate the entry by typing ctrl+Z. For further details concerning this procedure, see Variables.
   You may assign any valid variable name to the mass; QMTools recognizes a mass entry by how it is used in other expressions, not by the assigned name.
   If Flex Units are adopted, no mass value is required and this step can be skipped.
3. On the Math Palette, enter a formula for the potential energy function using the standard rules for formula entry (see Functions for further details). You are free to use whatever function and argument names you wish; standard usage would dictate V(x). When you are finished, type ctrl+Z to validate the entry.
   Once defined, the potential energy function can be graphed by right-clicking anywhere in the formula field and selecting Plot Function from the popup menu. This brings up the Domain Editor. Be aware that the variable range and number of points you enter here will be used to calculate any quantum wavefunctions, as well as the potential energy.

Back to Top

Quantum Wavefunctions: Stationary States

With assignments of particle mass and potential energy, any number of stationary state waves (solutions to Schrödinger's time-independent equation) can be created, either in the Applet Editor or from within a running applet.

1. On the Math Palette, define a variable that will serve as the stationary state energy, and assign it a value (this can be changed later). Remember to register your entry by typing ctrl+Z.
2. Now enter a name for the stationary wave function, say ψ(x), and assign to it the expression sta(V(..), mass, E, x, t). Here "V" is the name of the potential function, "mass" is the particle mass, "E" is the name of the energy variable defined in the previous step, and "x" is the independent variable name. The final argument is optional; if included, it specifies the time. Using the reserved variable name "t" for this entry allows the waveform to be propagated with the Animator – see Animation for more on this feature.
   For ψ(x) to be an acceptable wavefunction, it must be everywhere bounded and continuous, properties that generally follow only if the energy is properly chosen – see Eigen-Energies for a systematic approach to finding the desired value(s).
   Creating a stationary wave in the Applet Editor is especially quick and easy: from the ShortCut Toolbar click the command button labeled ψ(..) to add the wavefunction and its associated energy to the Math Palette in one operation.
3. QMTools also can work with stationary states of 3d systems having spherically symmetric potentials. The stationary state in this case, say ψ(x, y, z), would be assigned to the expression sta3(g(..), em, x, y, z, t). Here "g" references the radial wave g(r) and "em" is the magnetic quantum number. g(r) is itself a stationary wave, and would be assigned to the expression sta(V(..), mass, ell, E, r, t) for the given potential energy (now V(r)) and mass. "E" again is the state energy, and "ell" specifies the orbital quantum number for this radial wave.
   As with other stationary waves, creating a radial wave in the Applet Editor is particularly simple: from the ShortCut Toolbar click the command button labeled g(..) to add the radial wavefunction, its associated energy, and the orbital quantum number to the Math Palette, all in one operation.
   QMTools recognizes radial waves programmatically by the value at the left endpoint of the coordinate interval. If this value is exactly zero (as it must be for radial waves), the stationary state is found as the solution to the radial wave equation, and the orbital quantum number is identified as the 4th parameter in the argument list. An error is reported if the number of function arguments listed is incompatible with the type of stationary wave expected.
4. If desired, the stationary wave can be graphed by right-clicking anywhere in its formula field and selecting Plot Function from the popup menu.

Back to Top

Quantum Wavefunctions: Non-Stationary States

Non-stationary states are interesting for their time-dependence. Such states can be created in the Applet Editor or from within a running applet. The procedure for creating a non-stationary state depends on how the initial wave is specified.

1. If the intial wave is presented as a mixture of stationary states specified by an envelope function, say a(E), we find the non-stationary state using the built-in support provided by the spectral filter "spf(...)" and the spectral transform "spt(...)". The former takes the envelope function and passes only those values for which the argument matches a stationary state energy (consistent with the given potential energy and mass). The filtered result is then passed to the spectral transform, which constructs a non-stationary wave by adding stationary waves, each weighted by the surviving amplitude for that energy.

   Example:

   Suppose we wish to construct a non-stationary wave as an equal admixture of all stationary waves with energies lying between E_min and E_max. Assuming the potential energy function and particle mass have already been assigned (as V(x) and mass, respectively), we would add the following assignments to the Math Palette: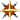

   a(E) ≡ 1
   φ(E) ≡ spf(V(..), mass, a(E))
   ψ(x) ≡ spt(φ(..), x, t)

   To obtain the desired result, the domain of the [continuous] energy variable E must be limited to the interval [E_min, E_max] (see Variables for how to set a variable's domain). The uniform envelope function a(E) ensures that all stationary states are weighted equally in the mixture. Note, too, that ψ(x) constructed this way is automatically normalized, and – because it references the time parameter t – is subject to Animation.
2. In the preceding example, the initial state is specified by its spectral wavefunction φ(E). More often, we would know the coordinate-space wavefunction φ(x); in that case, the non-stationary state is constructed using the built-in propagator "adv(...)".

   Example:

   Suppose we wish to construct the non-stationary wave that evolves from the initial [gaussian] wave exp(−x²). Again, assuming the potential energy function and particle mass have already been assigned as V(x) and mass, respectively, we would add the following assignments to the Math Palett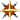e:

   φ(x) ≡ exp(−x²)
   ψ(x) ≡ adv(V(..), mass, φ(..), x, t)

   The propagator preserves normalization, but since the initial wave is not normalized, neither is ψ(x). As before, Animation is used to propagate this wave forward (or backward) in time.
   QMTools propagates these waves using the Crank-Nicholson scheme, and employs a fifth order Numerov algorithm for the spatial integration. As is well known, the Crank-Nicholson discretization conserves probability and energy, and is stable (though perhaps inaccurate) for any choice of space and time increments. The latter is set internally based on the energy of the initial wave.
   The initial wave is taken to be zero outside its interval of definition; for that reason it also should be nearly zero at the boundaries so as to avoid introducing discontinuities (which can give rise to spurious effects during evolution).
   The boundary conditions applied at the interval endpoints are one of two types: for states that remain confined, rigid-wall boundary conditions are adequate; transparent boundary conditions are necessary when the propagating wave is not confined, as happens in scattering situations. Transparent boundary conditions simulate a spatial region of infinite extent, thus eliminating any spurious reflections at the (arbitrary) interval endpoints. The choice of boundary conditions is made programmatically; transparent boundary conditions are used only when needed, since they incur a computational penalty that becomes noticeable after many time steps.

Back to Top