Math Basics Math Menus Functions Variables Built-in Math Animation
Graph Basics Plot Markup Graph Slicing
QM Waves Eigen-Energies Scattering QM Statistics QM Math
QMTools recognizes several mathematical and physical constants, as well as numerous operators and functions. The latter include most commonly used functions of mathematics, as well as a variety of special functions important in scientific applications.

Reserved Constants
The mathematical constants e (base of natural logarithms) and π (Euclidean ratio of circle circumference to diameter) have predefined values.
- e = 2.718281828459045...
- π = 3.141592653589793...

Standard Mathematical Functions
Most functions accept a complex argument, indicated by "z" in the usage column below; all others take real arguments only.
| Description | Usage |
|---|---|
| Sine | sin(z) |
| Cosine | cos(z) |
| Tangent | tan(z) |
| Arc Sine | asin(z) |
| Arc Cosine | acos(z) |
| Arc Tangent | atan(z) |
| Hyperbolic Sine | sinh(z) |
| Hyperbolic Cosine | cosh(z) |
| Hyperbolic Tangent | tanh(z) |
| Inverse Hyperbolic Sine | asinh(z) |
| Inverse Hyperbolic Cosine | acosh(z) |
| Inverse Hyperbolic Tangent | atanh(z) |
| Exponential | exp(z) |
| Natural Logarithm | ln(z) |
| Logarithm base 10 | log(z) |
| Absolute Value | abs(x) or |x| |
| Heaviside Step | hvs(x) |
| Random Number on (0, 1) | rand() |
| Real Component | re(z) |
| Imaginary Component | im(z) |
| Complex Argument (radians) | arg(z) |
| Complex Modulus | cmod(z) |
| Complex Conjugate | conj(z) |

Special Function Support
Special function values are computed to an accuracy of better than 1 part in 106 (and often much better than this).
| Description | Usage | Comments |
|---|---|---|
| Airy Function Ai | airyAi(x) | x real |
| Airy Function Bi | airyBi(x) | x real |
| Airy Function Gi | airyGi(x) | x real |
| Airy Function Hi | airyHi(x) | x real |
| Bessel Function Jν | besselJ(ν, x) | ν real; x > 0 |
| Bessel Function Yν | besselY(ν, x) | ν real; x > 0 |
| Dawson's Integral | daw(x) | x real |
| Factorial Function | fac(n) or n! | 0 ≤ n ≤ 12; n integer |
| Fresnel Auxiliary f | fresnelF(x) | x > 0 |
| Fresnel Auxiliary g | fresnelG(x) | x > 0 |
| Legendre Polynomial Pn | legendre(n,x) | 0 ≤ n ≤ 9; Pn(1) = 1 |

Operators
Operator support extends beyond the familiar arithmetic operations (addition, multiplication, etc.), to include roots, conditionals, and summation.
- Arithmetic operations are inserted in context by typing the expected characters:
'+' (addition), '−' (subtraction),
'*' (multiplication), '/' (division),
and '^' (exponentiation).
 Multiple operations are evaluated in the order of their precedence,
which can be clarified or overridden by surrounding parentheses. An existing node
may be enclosed in parentheses by selecting it and typing
ctrl+9.
Multiple operations are evaluated in the order of their precedence,
which can be clarified or overridden by surrounding parentheses. An existing node
may be enclosed in parentheses by selecting it and typing
ctrl+9.
- Roots may be found using the operator for exponentiation: for example, you would enter 2.50.25 to calculate the 4th root of 2.5. For the special case of square roots, QMTools offers the added convenience of the root symbol (available from the Insert item of the formula popup menu) and filling in the operand.
- Conditionals refer to structures where the result is contingent upon a
condition.
The function f(x) which is zero to the left of the origin and unity to the right (Heaviside step function) is defined on the Math Palette by the following statement: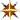 Example:f(x) ≡ x < 0 → 0 | 1This statement has the general form:expr1 → expr2 | expr3where expr1 refers to a boolean expression. The right arrow is made by typing ctrl+A; typing the backslash character '\' inserts the vertical bar. Evaluation proceeds as follows: expr1 is evaluated; if the value is true, then the value of expr2 is returned; otherwise the value of expr3 is returned.
Example:f(x) ≡ x < 0 → 0 | 1This statement has the general form:expr1 → expr2 | expr3where expr1 refers to a boolean expression. The right arrow is made by typing ctrl+A; typing the backslash character '\' inserts the vertical bar. Evaluation proceeds as follows: expr1 is evaluated; if the value is true, then the value of expr2 is returned; otherwise the value of expr3 is returned.Conditional statements also can be nested to produce more complicated forms, as illustrated below.
A function g(x) that evaluates to unity for 0 < x < 1 and is zero otherwise would be defined on the Math Palette by the statement: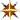 Example:g(x) ≡ x ≤ 0 → 0 | x < 1 → 1 | 0
Example:g(x) ≡ x ≤ 0 → 0 | x < 1 → 1 | 0 - Summation requires a special 'under-over' structure that is readily
inserted by typing the keyboard shortcut alt+ctrl+S.
To generate the formula for summing the quantity 2n + 1 from n = 0 to n = 4, you would do the following: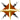 Example:
Example:- Type alt+ctrl+S to insert the summation symbol, along with a template for the limit fields and the expression to be summed (the summand). The cursor is left in the limit stop field.
- Type "4", followed by a right arrow to move the cursor to the limit start field.
- Next type "0", followed by the up arrow to move the cursor to the summand field.
- Lastly, type the open parenthesis "(" (creates the group consisting of both an open and a close), followed by the summand "2n + 1".