d'Alembert Solution of the Wave Equation
Dr. R. L. Herman
This is a summary of solutions of the wave equation based upon the
d'Alembert solution. This is meant to be a review of material
already covered in class. We begin with the general solution and
then specify initial and boundary conditions in later sections.
This will show the tie between the various solutions covered in
class, and some of those not covered in detail. We end with
examples of animations done in Maple 6.
Postscript file
1 General Solution
We start with the wave equation
which was derived in class for small amplitude vibrations of a
uniform string under a constant tension.
Making the substitutions x = x+ct and h = x-ct, this
equation is transformed to
This equation can be integrated to find solutions take the form of
a sum of a wave traveling to the right and one traveling to the
left:
|
u(x,t) = F(x)+G(h), or u(x,t) = F(x+ct)+G(x-ct), |
| (3) |
where F and G are arbitrary functions that can be determined
from prescribed initial and boundary conditions. We will review
these in the next sections.
2 Initial Conditions
The wave equation (1) is second order in time.
Therefore, we need two initial conditions, specifying the initial
position u(x,0) and the initial velocity ut(x,0) of each
point on the string. Thus, we assume
|
u(x,0) = f(x), ut(x,0) = g(x). |
| (4) |
Imposing these conditions on the general solution (3),
we have
Integrating the second equation, we obtain a second equation for
the unknown functions, F(x) and G(x).
|
F(x)-G(x) = |
1
c
|
|
ó
õ
|
x
0
|
g(s) ds +F(0)-G(0). |
| (7) |
Adding and subtracting to Equation (5), we
find general forms for our unknown functions:
|
|
|
F(x) = |
1
2
|
f(x) + |
1
2c
|
|
ó
õ
|
x
0
|
g(s) ds + |
1
2
|
[ F(0)-G(0) ], |
| (8) | | G(x) = |
1
2
|
f(x) - |
1
2c
|
|
ó
õ
|
x
0
|
g(s) ds - |
1
2
|
[ F(0)-G(0) ]. |
| (9) |
| |
|
Now, the solution to the wave equation satisfying our initial
conditions, can be written
|
| |
|
|
| |
|
|
1
2
|
[f(x+ct)+f(x-ct)] + |
1
2c
|
|
ó
õ
|
x+ct
x-ct
|
g(s) ds. |
| (10) |
| |
|
Note that F(0) and G(0) do not appear in this physical
solution. Therefore, we will drop them in the rest of this
discussion.
3 Boundary Conditions
The problem is that the solution in (10) only makes sense
for the part of the interval [x-ct, x+ct] contained in the
domain of f and g. This is fine if these domains are the
entire real axis. However, there are problems for smaller domains.
In such cases we will needed to make use of the boundary
conditions to get to the solution of the initial-boundary value
problem.
3.1 Infinite String
For f(x) and g(x) defined on -¥ < x < ¥, such as in
the case of an infinite string, the solution (10) is
well-defined.
|
| |
|
|
| |
|
|
1
2
|
[f(x+ct)+f(x-ct)] + |
1
2c
|
|
ó
õ
|
x+ct
x-ct
|
g(s) ds. |
| (11) |
| |
|
3.2 Semi-infinite String
For f(x) and g(x) defined on 0 £ x < ¥, such as in the
case of the semi-infinite string, the solution (10) is not
well-defined. For positive c and t > 0, we have that f(x-ct) is
not defined for x-ct < 0, or t > x/c. This also affects the range
of integration over values where g is not defined.
This can be seen using characteristics in the xt-plane.
Information from the point x = 0 can only propagate to the right
at speed c. Drawing the line x = ct, we find that values for
u(x,t) can only be obtained from the initial condition alone if
the point (x,t) lies below the characteristic. In order to get
values for points above the characteristics, we need to specify
information, which will propagate from that region. Specifying
values along the t-axis will provide such information. Namely,
we need to specify a boundary condition at x = 0.
Two types of boundary conditions are that a) the end is fixed,
u(0,t) = 0, t ³ 0, or b) the end is free ux(0,t) = 0, t ³ 0. We will treat each case separately.
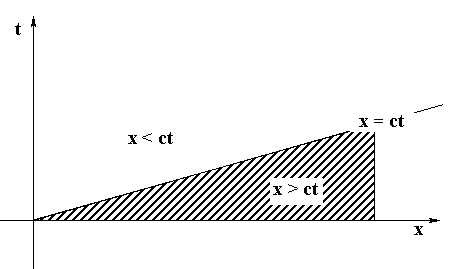
For a fixed end, u(0,t) = 0, t ³ 0, we have
|
0 = u(0,t) = F(ct)+G(-ct). |
| (12) |
Letting z = -ct, this equation can be rewritten as
This equation extends the range of G to negative values and can
then be used to do the same for F. Inserting the expressions for
F and G from Equations (8)-(9), we have
|
| |
|
|
|
|
1
2
|
f(z) - |
1
2c
|
|
ó
õ
|
z
0
|
g(s) ds, |
| (14) | |
|
|
- |
1
2
|
f(-z) - |
1
2c
|
|
ó
õ
|
-z
0
|
g(s) ds |
| |
|
| - |
1
2
|
f(-z) + |
1
2c
|
|
ó
õ
|
z
0
|
g(-s) ds |
| (15) |
| |
|
Comparing the expressions in (14) and (15), we see
that we can satisfy (13) if
|
f(z) = - f(-z), and g(z) = -g(-z). |
| (16) |
In other words, we can extend the functions f and
g to be odd functions with respect to x = 0.
For a free end, ux(0,t) = 0, t ³ 0, we have
|
0 = ux(0,t) = F¢(ct)+ G¢(-ct). |
| (17) |
Letting z = -ct, this equation can be rewritten as
Inserting the expressions for F and G from Equations
(8)-(9), we have
|
| |
|
|
| (19) | |
|
| - |
1
2
|
f¢(-z) - |
1
2c
|
g(-z). |
| (20) |
| |
|
Comparing these expressions, we see that we can satisfy
(18) if
|
f¢(z) = - f¢(-z), and g(z) = g(-z). |
| (21) |
This means that the function f¢ needs to be an odd function
with respect to x = 0. Thus, the functions f and g need to be even functions
with respect to x = 0.
3.3 Finite String
In this case we have a physical string, which has a finite length
l. We first consider the propagation of information from the
initial conditions along the characteristics. f and g are
defined for 0 £ x £ l. The general solution (10)
is of the form F(x+ct)+G(x-ct). Thus, we can only compute F
for 0 £ x+ct £ l and G for 0 £ x-ct £ l. For
t ³ 0, we then have t < [(l-x)/ c] and t < x/c,
respectively.
The region defined by these inequalities is a triangular region.
This region contains all points whose solution can be obtained
using only the initial conditions. In order to obtain more
information about the future values of the solution, we need to
specify boundary conditions at x = 0 (to give G) and x = l
(to give F).
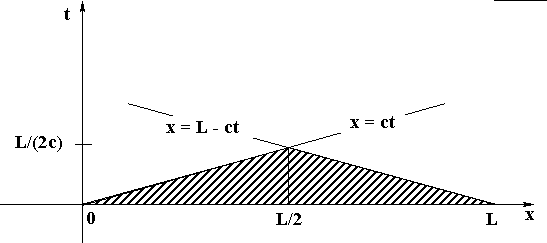
In either case we can specify fixed or free ends. We have seen
previously what this means for x = 0:
We now consider the conditions at x = l.
3.4 Conditions at x = l
For a fixed end, u(l,t) = 0, t ³ 0, we have
|
0 = u(l,t) = F(l+ct)+G(l-ct). |
| (24) |
Letting z = l+ct, this equation can be rewritten as
This equation extends the range of F to values l £ z £ 2l. Inserting the expressions for F and G from
Equations (8)-(9), we have
|
| |
|
|
|
|
1
2
|
f(z) + |
1
2c
|
|
ó
õ
|
z
0
|
g(s) ds, |
| (26) | |
|
|
- |
1
2
|
f(2l-z) + |
1
2c
|
|
ó
õ
|
2l-z
0
|
g(s) ds |
| |
|
| - |
1
2
|
f(2l-z) - |
1
2c
|
|
ó
õ
|
z
2l
|
g(2l-t) dt. |
| (27) |
| |
|
Comparing these expressions, we see that we can satisfy
(25) if
and
|
|
ó
õ
|
z
0
|
g(s) ds = - |
ó
õ
|
z
2l
|
g(2l-t) dt. |
| (29) |
Differentiating the last expression with respect to
z, we obtain
These conditions on f and g mean that we can
extend these functions to l £ z £ 2l by
performing and odd extension about x = l. This is very similar
to the case encountered for a fixed end at x = 0.
For a free end, ux(l,t) = 0, t ³ 0, we have
|
0 = ux(l,t) = F¢(l+ct)+ G¢(l-ct). |
| (31) |
Letting z = l+ct, this equation can be rewritten as
|
F¢(z) = -G¢(2l-z), z ³ l. |
| (32) |
Inserting the expressions for F and G from Equations
(8)-(9), we have
|
| |
|
|
| (33) | |
|
| - |
1
2
|
f¢(2l-z) + |
1
2c
|
g(2l-z). |
| (34) |
| |
|
Comparing these expressions, we see that we can satisfy
(18) if
|
f¢(z) = - f¢(2l-z), and g(z) = g(2l-z). |
| (35) |
This means that the function f¢ needs to be an odd function
with respect to x = l. Thus, the functions f and g need to be even functions
with respect to x = l.
3.4.3 Tying Loose Ends
Now all we need to do is look at the different possibilities for
the ends. We could have two fixed ends, two free ends, or one free
and one fixed. With each case we use the results for the type of
extensions for f(x) and g(x). These will lead to certain types
of periodic extensions for these functions, which can be used to
rewrite the general solution as a well defined solution to the
problem over the finite interval.
- Two Fixed Ends
In this case we have the conditions
|
|
|
f(x) = -f(-x), -l £ x £ 0 |
| | f(x) = -f(2l-x), l £ x £ 2l. |
| (36) |
| |
|
Then
|
f(x+2l) = -f(2l-(x+2l)) = - f(-x) = f(x). |
|
Thus,
we see that f and g need to be periodic odd extensions of the
original functions with period 2l.
- Two Free Ends
In this case we have the conditions
|
| |
| | f(x) = f(2l-x), l £ x £ 2l. |
| (37) |
| |
|
Then
|
f(x+2l) = f(2l-(x+2l)) = f(-x) = f(x). |
|
Thus, we
see that f and g need to be periodic even extensions of the
original functions with period 2l.
- One Fixed End and One Free End
In this case we either have the conditions (fixed at x = 0)
|
|
|
f(x) = -f(-x), -l £ x £ 0 |
| | f(x) = f(2l-x), l £ x £ 2l. |
| (38) |
| |
|
or we have the conditions (free at x = 0)
|
| |
| | f(x) = -f(2l-x), l £ x £ 2l. |
| (39) |
| |
|
In the first case,
Thus, we see
that f and g need to be periodic odd extensions of the
original functions with period 4l, since f is an odd
extension about x = 0.
Similarly, for the second case,
|
| |
|
|
|
-f(2l-(x+4l)) = -f(-x-2l) |
| |
|
| |
|
| (41) |
| |
|
Thus, we see that f and g need to be periodic even extensions
of the original functions with period 4l, since f is an
even extension about x = 0.
3.5 Examples
Here are some examples in Maple:
Example 1 HTML version, Maple
version
(Examples for two fixed ends)
Example 2 HTML version, Maple
version
(Examples for one end fixed and the other free)
Example 3 HTML version, Maple
version (Presentation of the odd extensions needed to solve the problem of
two fixed ends with g(x)=0.)
File translated from TEX by TTH, version 2.25.
On 13 Sep 2000, 08:11.


