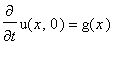d'Alembert's Solution to the Wave Equation

> restart: with(plots): Mod:=(x,y)->x-floor(x/y)*y:

A string of length L is fixed at both ends with initial conditions and 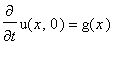. d'Alembert's solution to the wave equation is given by the expression u(x,t) below with and the odd periodic extensions of period 2L of f and g.

> u:=(x,t)->1/2*(fp(x+c*t)+fp(x-c*t))+1/(2*c)*int(gp(z),z=x-c*t..x+c*t);

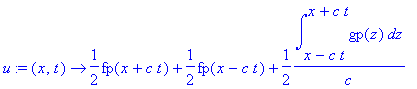
The odd extensions are obtained by first extending f and g to odd functions about . This gives one period of the extension.

> fodd:=x->piecewise(x<=L,f(x),x>L,-f(2*L-x)); godd:=x->piecewise(x<=L,g(x),x>L,-g(2*L-x));

Now, the functions are extended as periodic functions over the entire real line.

> fp:=x->fodd(Mod(x,2*L)); gp:=x->godd(Mod(x,2*L));

Example 1: For a simple example, one finds that the above functions are defined correctly.

> L:=2: f:=x->x*(L-x); g:=0:

> plot({f(x),g(x)},x=0..L,color=[blue,red]);

> plot({fodd(x),godd(x)},x=0..2*L,color=[blue,red]);

> plot({fp(x),gp(x)},x=-2*L..3*L,color=[blue,red]);

The solution to the wave equation can be animated. Click on the graph below and then on the play button

> c:=.2: animate( u(x,t),x=0..L,t=0..20,frames=50,color=blue);

Here are other examples:

> L:=2:c:=.2: f:=x->piecewise(x<L/2,x*(L/2-x),x>L/2,0): g:=x->0:
animate( u(x,t),x=0..L,t=0..20,frames=50,color=blue);

> L:=2:c:=.2:a:=L/4: f:=x->piecewise(x<=a,x/a,x>a,(L-x)/(L-a)): g:=x->0:
animate( u(x,t),x=0..L,t=0..20,frames=50,color=blue);

> L:=2:c:=.2:a:=L/2: f:=x->sin(Pi*x/L): g:=x->0:
animate( u(x,t),x=0..L,t=0..20,frames=50,color=blue);

> L:=2:c:=.2:a:=L/2: f:=x->sin(2*Pi*x/L): g:=x->0:
animate( u(x,t),x=0..L,t=0..20,frames=50,color=blue);

> L:=2:c:=.2:a:=L/2: f:=x->sin(Pi*x/L)+.5*sin(2*Pi*x/L): g:=x->0:
animate( u(x,t),x=0..L,t=0..20,frames=50,color=blue);

Try your own initial conditions and play with the wavespeed c.