d'Alembert's Solution for

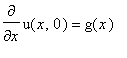A string of length L is fixed at both ends with initial conditions and . d'Alembert's solution to the wave equation is given by , where F(x) and G(x) are determined from the odd extensions of f(x) and g(x) about both and .

In this example, we will consider an initial profile with zero initial velocity. We will see how one puts together the odd extensions to form an odd periodic extension of f(x) with period 2*L . This periodic function can then be used to produce the desired solution of the wave equation.

> restart: with(plots): Mod:=(x,y)->x-floor(x/y)*y:

Warning, the name changecoords has been redefined

Let f(x) be the function defined on [0,L]. We first extend it to f1(x) , which is defined on [0,2L] and is odd about .

> f:=x->piecewise(x<=a,x/a,x<=L,(L-x)/(L-a));
f1:=x->piecewise(x<=L,f(x),x<=2*L,-f(2*L-x));

> a:=L/4: L:=1: plot(f(x),x=0..L,title=`Initial Profile u(x,0)`);

> plot(f1(x),x=0..2*L,title=`Extension to [0,2L]`);

Now we fully extend f(x) to the entire real line as a periodic function of period 2*L . From d'Alembert's solution with , we can write down F(x), G(x) and the solution u(x,t) . First we obtain F and G (which are the same in this example) :

> F:=x->1/2*f1(Mod(x,2*L)); G:=x->-F(-x);

We plot F and , which is the "taller" of the two functions.

> plot({F(x), F(x)+G(x)},x=-4*L..4*L,color=[blue,red]);

As t increases, we can look at the sum of the left and right traveling waves for a unit speed. In the plot below u has been vertically shifted for visualization purposes.

> t:=0.6:
plot({F(x+t), G(x-t),F(x+t)+G(x-t)+1,1},x=-4*L..4*L,color=[blue,red, green]);

Animation of the above functions over one period of time. Try to visualize the right and left traveling waves in the lower portion of the plot.

> t:='t': animate({F(x+t), G(x-t),F(x+t)+G(x-t)+1,1},x=-4*L..4*L,t=0..4, numpoints=100,frames=50,color=blue);

Animation of the solution over the physical interval [0,L].

> t:='t': animate(F(x+t)+G(x-t),x=0..L,t=0..4, numpoints=200,frames=100,color=blue,title=`u(x,t)`);

>

>