ODE.mws
Maple Operations for ODEs I
Always start with this command. It clears the internal memory.
Basic Calculus
In this section we remind you how to differentiate and integrate functions. First place the expression in a variable. Then you can differentiate and integrate this expression.Note that this is not in the form of a function that can easily be evaluated.
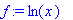
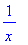
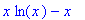
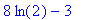
Solving ODEs
Many differential equations can be solved by Maple, though sometimes the answer may not seem to be in the form you might expect. Here is the simplest way to find a solution using dsolve.
Help on dsolve
One can put the equation in a variable and then use dsolve, or one can do it in one line by placing the equation directly into dsolve. Note the need to express the dependent variable as a function of the independent variable.
| > |
ODE:=diff(y(x),x)=x*y(x);
|
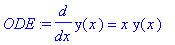
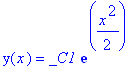
To find a particular solution, one can insert the initial condition. Note the use of the curly braces.
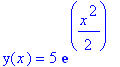
One can verify a solution. For example, you could get a solution by hand and then verify it in Maple.
| > |
eval(subs(y(x)=A*exp(x^2/2),ODE));
|
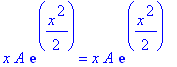
Plotting Solutions
Often one is interested in the behavior of the solution. One can graph the solution. Here is how one can take the result of dsolve and plot it.
Using the unapply operation, one can take the right hand side of the result (as seen in the last section) and give it a name.
Help on unapply
Then plot it as a function.
Help on plot
| > |
f:=unapply(rhs(dsolve({ODE, y(0)=3})),x);
|
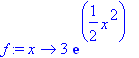
![[Maple Plot]](images/ODE10.gif)
The unapply function is useful if further need is to be made of the function. However, you can just as easily place the right hand side of the solution in a simple variable and then plot it, or just put this expression directly into the plot function.
| > |
g:=rhs(dsolve({ODE, y(0)=3}));
|
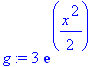
![[Maple Plot]](images/ODE12.gif)
Even if you cannot get a closed form solution, you can get a plot by numerically solving the equation. In the library [plots] is the function odeplot. Here is one example of its use.
Library [plots]
Warning, the name changecoords has been redefined
| > |
p:= dsolve({ODE, y(0)=3}, y(x),type=numeric):
|
| > |
odeplot(p,[x,y(x)],0..1);
|
![[Maple Plot]](images/ODE13.gif)
Plotting with DEPlot
Maple has a powerful set of routines for solving differential equations. These are in the
DEtools
library.
Here is the basic form for using
DEplot
. In this case all relevant arguments are placed into the operation. Later will will see what the arrows option means.
| > |
DEplot(diff(y(x),x)=y(x)*(y(x)-5),y(x),x=-1..1,y=-2..8,[[y(0)=1]],arrows=none);
|
![[Maple Plot]](images/ODE14.gif)
You could also cleanup the above by specifying some arguments using variables. Also, you can change the linecolor.
| > |
ode:=diff(y(x),x)=y(x)*(y(x)-5):
ics:=[[y(0)=1]]:
DEplot(ode,y(x),x=-1..1,y=-2..8,ics,linecolor=black,arrows=none);
|
![[Maple Plot]](images/ODE15.gif)
Of course, you can put in several initial conditions so that you can see members of the family of solutions.
| > |
DEplot(diff(y(x),x)=y(x)*(y(x)-5),y(x),x=-1..1,y=-2..8,[[y(0)=1],[y(0)=-2],[y(0)=8]],linecolor=black,arrows=none);
|
![[Maple Plot]](images/ODE16.gif)
You can also allow for arrows. What do these indicate?
| > |
DEplot(diff(y(x),x)=y(x)*(y(x)-5),y(x),x=-1..1,y=-2..8,[[y(0)=1],[y(0)=-2],[y(0)=8]],linecolor=black);
|
![[Maple Plot]](images/ODE17.gif)
This background is called a direction field.
| > |
DEplot(diff(y(x),x)=y(x)*(y(x)-5),y(x),x=-1..1,y=-2..8);
|
![[Maple Plot]](images/ODE18.gif)
The direction field may also be produced using
dfieldplot
. However, you cannot superimpose solutions as above.
| > |
dfieldplot(diff(y(x),x)=y(x)*(y(x)-5),y(x),x=-1..1,y=-2..8);
|
![[Maple Plot]](images/ODE19.gif)
![]()
![]()
![]()
![]()
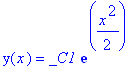
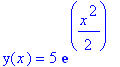
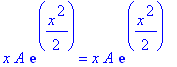
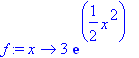
![[Maple Plot]](images/ODE10.gif)
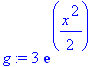
![[Maple Plot]](images/ODE12.gif)
![[Maple Plot]](images/ODE13.gif)
![[Maple Plot]](images/ODE14.gif)
![[Maple Plot]](images/ODE15.gif)
![[Maple Plot]](images/ODE16.gif)
![[Maple Plot]](images/ODE17.gif)
![[Maple Plot]](images/ODE18.gif)
![[Maple Plot]](images/ODE19.gif)