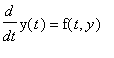Piecewise Functions in First Order ODEs

This is a sample worksheet showing how do plot slope (direction) fields for 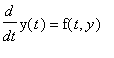, where f is a piecewise defined function. This can be done with the Heaviside  function or the piecewise  function.

Restart clears memory and with(DEtools) loads the differential equations plotting tools.

>	restart: with(DEtools):

Heaviside and Picewise Defined Functions

The Heaviside function is also called a step function. It gives 0 for arguments < 0 and 1 for arguments > 0.

>	plot(Heaviside(x),x=-2..2);

Shifting the function and adding or subtracting makes things piecewise defined functions.

>	plot(Heaviside(x)-Heaviside(x-3),x=-2..5);

The piecewise function performs the same way, but one needs to be careful of arguments. For now one does not yet need the Heaviside function.

>	plot(piecewise(x<0,0,x<3,1,0),x=-2..5);

RC Circuit Problems

Here we have a differential equation for the voltage across the capacitor, y(t). In this case f(t,y) is defined next with R the resistance in ohms, C the capacitance in farads and V(t) the power supply voltage. As V(t) can vary for different times, this can lead to a piecewise defined function for the observed time period.

>	f:=(y,t)->(V(t)-y)/(R*C);

>	R:=0.2: C:=1: K:=2: V:=t->0;

>	DEplot(diff(y(t),t)=f(y(t),t),y(t),t=0..6,y=0..4, title="No Voltage Source, V=0");

>

V:=t->K;

>	DEplot(diff(y(t),t)=f(y(t),t),y(t),t=0..6,y=0..4, title="Constant Voltage Source, V=2");

Consider turning the constant source on from t = 0 to t=3.

>	V:=t->piecewise(t<0,0,t<3,K,0);

>	DEplot(diff(y(t),t)=f(y(t),t),y(t),t=0..6,y=0..4,title="Constant Voltage Source \n Finite Duration");

One can even add initial consitions to see various solutions.

>	DEplot(diff(y(t),t)=f(y(t),t),y(t),t=0..6,y=0..4,[[y(1)=1],[y(0)=2],[y(1)=3],[y(4.1)=4]],linecolor=black,stepsize=.05,title="Constant Voltage Source -Finite Duration \n Display of Several Solutions");

>