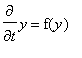Bifurcations

Begin with restart to clear memomry and packages DEtools and plots containing the DEplot and display, respectively.

>	restart: with(DEtools): with(plots):

Warning, the name changecoords has been redefined

Consider the autonomous differential equation 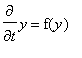 for the following function.

>	f:=y->y^2-5;

Note that this function has two roots, corresponding to equilibrium (or fixed point) solutions. This tells us that we expect three types of solution behaviors. For  and  the solution is an increasing function and for  the solution is decreasing.

>	plot(f(y),y=-3..3);

This can be seen from the slope field with several initial conditions displayed.

>	ics:=[[y(0)=-3],[y(0)=-2],[y(0)=-1],[y(0)=0],[y(0)=1],[y(0)=2],[y(0)=3]]: DEplot(diff(y(t),t)=f(y(t)),y(t),t=-6..6,y=-3..3,ics,stepsize=0.1);

Saddle-Node Bifurcation

This function is one in a family of functions of the form

>	f:=y->y^2+mu;

It is interesting to see the behavior of solutions as the parameter  is varied. first we see how  changes as the parameter is varied.
(Click on the figure and use the animations controls that will appear above.)

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."): P[i]:=plot(f(y),y=-3..3,title=str): od: display(seq(P[k],k=1..21),insequence=true);

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."): P[i]:=DEplot(diff(y(t),t)=f(y(t)),y(t),t=-6..6,y=-3..3,ics,title=str,stepsize=.1): od:

>	display(seq(P[k],k=1..21),insequence=true);

Note that the nature and number of the equilibrium solutions changes as the parameter increase. This change of behavior at  is called a bifurcation and this type of birfurcation is called a saddle-node bifurcation.

Transcritical Bifurcation

>	f:=y->mu*y-y^2;

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."): P[i]:=plot(f(y),y=-6..6,title=str): od: display(seq(P[k],k=1..21),insequence=true);

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."); P[i]:=DEplot(diff(y(t),t)=f(y(t)),y(t),t=-6..6,y=-6..6,ics,title=str,stepsize=.1): od:

>	display(seq(P[k],k=1..21),insequence=true);

Pitchfork Bifurcation - Subcritical

>	f:=y->mu*y+y^3;

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."): P[i]:=plot(f(y),y=-3..3,title=str): od: display(seq(P[k],k=1..21),insequence=true);

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."); P[i]:=DEplot(diff(y(t),t)=f(y(t)),y(t),t=-6..6,y=-3..3,ics,title=str,stepsize=.1): od:

>	display(seq(P[k],k=1..21),insequence=true);

Pitchfork Bifurcation - Supercritical

>	f:=y->mu*y-y^3;

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."): P[i]:=plot(f(y),y=-3..3,title=str): od: display(seq(P[k],k=1..21),insequence=true);

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."); P[i]:=DEplot(diff(y(t),t)=f(y(t)),y(t),t=-6..6,y=-3..3,ics,title=str,stepsize=.1): od:

>	display(seq(P[k],k=1..21),insequence=true);

Finding Equlibria and Classification

Some functions are not easily plotted such as the following example from the text:

>	f:=y->y*(cos(y^5+2*y)-27*Pi*y^4);

One could plot the function and locate equilibrium points (roots of f). In this case there are two with  the simplest.

>	plot(f(y),y=-.1..0.4);

One need only find the roots and look at the slopes at these points. Thus, one does not have to plot the function to classify points.

>	Df:=diff(f(y),y);

First we make sure of the first root. We see that the slope is positive, so  is a source .

>	x:=fsolve(f(y),y,-0.2..0.2); evalf(subs(y=x,Df));

The second root has a negative slope, so it is a sink .

>	x:=fsolve(f(y),y,0.2..0.4); evalf(subs(y=x,Df));

Determining Bifurcation Points

>	f:=y->y*(1-y)^2+mu;

Looking at f for different values of  leads to trying to understand what happens at the bifurcation points. For  there are two equilibrium solutions. If we change the parameter by a small amount we see a change in the number of equilibrium solutions.

>	plot({y*(1-y)^2-.5,y*(1-y)^2,y*(1-y)^2+.5},y=-1..2,color=black);

>	for i to 21 do mu:=(i-11)/2:str:=cat( "The value of mu is ",convert(mu,string), "."): P[i]:=plot(f(y),y=-1..2,title=str): od: display(seq(P[k],k=1..21),insequence=true);

There are two points at which 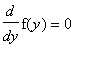. This is where the graph can be tangent to the horizontal axis.

>	mu:='mu': solve(diff(f(y),y)=0);

This occurs for the bifurcation parameter found by solving  for each point:

>	f(1)=0; f(1/3)=0;

Now you can following the solution behavior as the parameter moves into and out of the interval ( ).

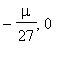>	ics:=[[y(0)=-2],[y(0)=-1],[y(0)=-0.5],[y(0)=0],[y(0)=0.5],[y(0)=1],[y(0)=2]]: for i to 21 do mu:=(i-11)/27:str:=cat( "The value of mu is ",convert(mu,string), "."): P[i]:=DEplot(diff(y(t),t)=f(y(t)),y(t),t=-3..3,y=-1..2.5,ics,title=str,stepsize=.05): od: display(seq(P[k],k=1..21),insequence=true);

>