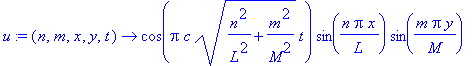
Rectangular Membrane

This worksheet allow one to plot modes of vibration for a rectangular membrane with fixed homogeneous boundary conditions and to visualize the vibrations in time. The rectangle is L by M and the wave speed is given by c.

> restart: L:=1: M:=1: c:=1: with(plots):

Warning, the name changecoords has been redefined

The product solutions take the folowing form for a zero initial velocity, though one can easily add a phase shift in time to simulate other motions.

> u:=(n,m,x,y,t)->cos(2*Pi*c/2*sqrt((n/L)^2+(m/M)^2)*t)*sin(n*Pi*x/L)*sin(m*Pi*y/M);

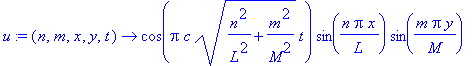
The frequency of oscillation of the nm-th mode is given by

> nu:=(n,m)->c/2*sqrt((n/L)^2+(m/M)^2);

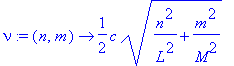
The initial profile of the membrane:

> n0:=1: m0:=1: plot3d(u(n0,m0,x,y,0),x=0..1,y=0..1);

The evolution of this profile

> animate3d(u(n0,m0,x,y,t),x=0..1,y=0..1,t=0..1/nu(n0,m0),frames=20);

The following code shows how to save animations as animated gifs. The first line sets up the plot to be gif and the third line reverts the plotting back oto the screen.

> plotsetup(gif,plotoutput=`mesh33.gif`,plotoptions=`height=200,width=200`):

> n0:=3: m0:=3: animate3d(u(n0,m0,x,y,t),x=0..1,y=0..1,t=0..1/nu(n0,m0),frames=20);

> plotsetup(inline);

>