|
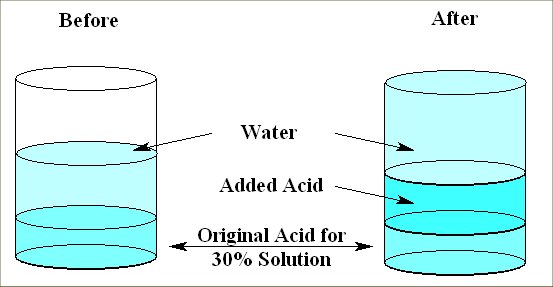
How many cubic centimeters of pure hydrochloric acid should be added to 20 cc of a 30% solution of hydrochloric acid to obtain a 50% solution? Let x = number of cc of pure acid. One can set up a table as below. In particular, you start with 20 cc (cubic centimeters = volume) of a 30% solution of acid. This means that 20(.30) = 6 cc is acid and the rest is water. If you add x cc of pure acid, then you have a new total volume of 20+x cc with 6+x cc of it acid. Thus, for it to be 50% of the total, one needs that (20+x)(.50) = 6+x cc of it acid. Solving for x, you should get x = 8 cc.
The below figure shows how one might visualize the relationship between the volume and concentration (percent of total volume) for putting a substance (acid) in water. Of course, the colors and separation of the acid and water are exaggerations in order to make a point. These mixtures are typically well mixed and are often colorless.
|
|||||||||||||||||
| E-Mail: Dr. Russell Herman | Last Updated: August 27, 2004 | ||||||||||||||||