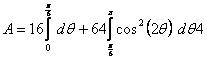Determine
what type of conic section is given by the equation 
. Put the equation in standard form and identify the
important relevant information. Sketch the curve on the grid below.Answers to MAT 162 Test 2 Sample Questions
Conic
1.
Determine
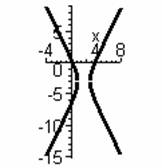
what type of conic section is given by the equation . Put the equation in standard form and identify the
important relevant information. Sketch the curve on the grid below.
Hyperbola
Standard form: 
center: 
vertices: 
, 
foci: 
, 
Parametric
2.
Below is shown the curve given parametrically by 
, 
over the parameter interval 
. Clearly label the initial point, the terminal point, and the
points corresponding to 
, 
and 
. Indicate the direction the curve is traced and how many
times the curve is traced (over the interval ).
3. Find the Cartesian equation for the curve given in Question #2.
4.
Find the derivative 
and the second derivative 
of the curve given in Question #2.
5.
Find the (Cartesian) equation of the line tangent to the curve given in
Question #2 at the point corresponding to .
6. Write the integral to find the length of one tracing of the entire curve given in Question #2. (Note: You do not need to evaluate the integral.)
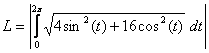
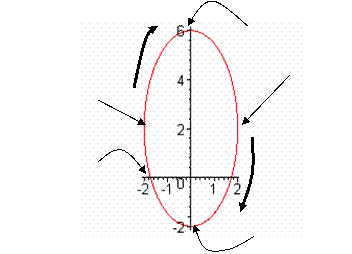
7. Write the integral to find the area inside the curve and below the x-axis, and evaluate this integral.
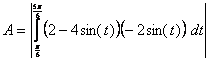
8. Write the integral to find the surface area of the solid generated by revolving the region in Question #7 around the x-axis. (Note: You do not need to evaluate the integral.)
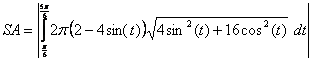
9. Write the integral to find the volume of the solid generated by revolving the region in Question #7 around the x-axis. (Note: You do not need to evaluate the integral.)
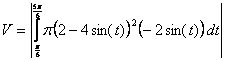
10.
Plot the point 
on the polar grid below. (Label the initial ray, and include
a scale with your plot.) Find two additional representations of this same point,
one with r > 0 and one with r < 0. (Note: angles which reduce to 
are not considered to be different from .)
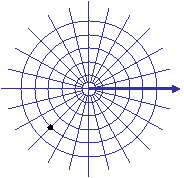
Note: there are many others
11.
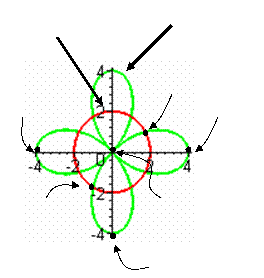Below
is shown the curves given by 
and 
. Identify which curve is which. Plot and label the points
corresponding to 
and 
on the curve given by 
.
12.
Find the derivative of .
13.
Find the (Cartesian) equation of the line tangent to the curve given by
at the point where 
.
14.
Set up the integral to find
the length of one tracing of . (Note: You do not need to evaluate the integral.)
15.
Set up the integral to find the area of the region inside the curve given
by and outside the curve given by . (Note: You do not need to evaluate the integral.)
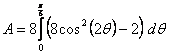
16.
Set up the integral to find the area of the region inside both curves
(where they overlap) and , and evaluate this integral.
