UNCW HIGH SCHOOL

MATH CONTEST

 

Department of Mathematics and Statistics

 

April 10, 2002

 

Scoring

 

Each question answered correctly scores 4 points.

Each question left blank scores 1 point.

Each question answered incorrectly scores 0 points.
 
 

 

 

 

 

 

 

 

 

 

 

 


High School Mathematics Contest Spring 2002

 

 

 

1.

Determine k so that the line containing the points and  is parallel to the line containing the points  and .

 

 

A)

-8.5

B)

-7.75

C)

2.25

D)

3.5

E)

23.75

 

 

 

2.

Determine which of the following is the same as

 .

 

 

A)

B)

C)

D)

E)

 

 

 

3.

The solution set to the system of inequalities  is given by

 

 

 

 

 

 

 

A)

the region shaded A

 

B)

the region shaded B

 

C)

the region shaded C

 

D)

the region shaded D

 

E)

the point (3,1)

 

 

4.

Simplify

.

 

 

A)

B)

C)

D)

E)

 

 

5.

If a and b are distinct primes other than 3, determine the number of positive divisors of 9a3b2.

 

 

A)

3

B)

24

C)

36

D)

64

E)

128

 

 

6.

Simplify

.

 

 

A)

B)

C)

D)

E)

 

 

7.

A rectangular box with volume 320 ft is built with a square base and top. The cost is $1.50 per ft for the bottom, $2.50 per ftfor the sides and $1 per ftfor the top.  Express the cost of the box as a function of the base side length x.

 

 

A)

 

B)

 

C)

 

D)

 

E)

 

 

8.

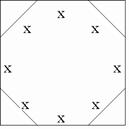
Find the area of the regular octagon inscribed in a square with side length 1.  Round your answer to the nearest hundredth.

 

 

 

 

A)

.67

B)

.78

C)

.83

D)

.88

E)

.92

 

 

9.

If the point (1,2) is on the graph of , determine which of the following must be a point on

 

 

A)

(-1,6) 

B)

(-1,5) 

C)

(3,3)

D)

(3,5)    

E)

(9,6)

 

 

 

10.

The average cost of moving a distance of 1255 miles is $1035 if you handle the move yourself.  This is about 52% of the cost of hiring a professional moving company.  Determine the cost of a move with the professional company, rounded to the nearest dollar.

 

 

A)

538

B)

1573

C)

1990

D)

2356   

E)

2413

 

 

 

11.

Given the sets , , and determine the set .

 

 

A)

{1}

 

B)

{1,6}

 

C)

{1,9}

 

D)

{1,6,9}

 

E)

{1,2,4,5,6,7,8,9}

 

 

 

12.

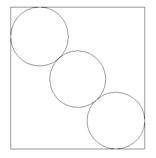
Each of the three circles in the figure have radius 1, and their centers lie on the diagonal of the square shown.  In addition, each of the two “outer” circles is tangent to two sides of the square and to the middle circle.  Compute the area of the square.

 

 

A)

6

B)

C)

D)

E)

 

 

13.

Solve the equation  for x. 

 

 

A)

B)

C)

D)

E)

 

 

 

14.

The minute hand of a clock is 6 inches long.  Find the distance the tip of the minute hand moves in 15 minutes.

 

 

 

A)

B)

C)

D)

E)

 

 

 

15.

In a survey of 100 stock market investors, it was found that 55 owned shares in IBM, 45 owned shares in AT&T, 40 owned shares in GE, 20 owned shares in both IBM and GE, 15 owned shares in both AT&T and GE, 20 owned shares in both IBM and AT&T, and 5 owned shares in all three companies.  Determine how many of the investors in the survey did not own shares in any of the three companies.

 

 

A)

0

B)

5

C)

10

D)

15

E)

20

 

 

 

16.

Simplify

.

 

 

A)

B)

C)

-

D)

E)

 

 

 

17.

Given that , determine .

 

 

 

A)

16

B)

20

C)

48

D)

64

E)

80

 

 

18.

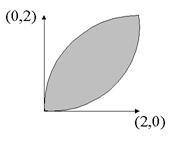
Circles of radius 2 with centers at (2,0) and (0,2) overlap in the shaded area shown in the figure.  Compute this area.

 

 

A)

B)

C)

D)

E)

 

 

 

19.

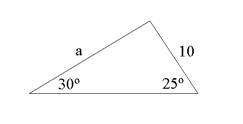
Determine the side labeled a for the triangle shown in the figure.

 

 

A)

 

 

B)

 

 

C)

 

D)

 

E)

 

 

20.

An operation * is defined for any integers a and b by .  Determine .

 

A)

0

B)

2

C)

9

D)

24

E)

30

 

 

21.

If the length of an edge of a cube is increased by 20%, determine the percent increase in the volume of the cube.  Express your answer to the nearest whole number.

 

 

A)

20

B)

43

C)

60

D)

73

E)

80

 

 

22.

 

 

 

The following bar graph  compares the volume of trading on the New York Stock Exchange and Nasdaq Stock Market.  Determine the first year the combined volume of both markets exceeded 500 billion shares.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A)

1992

B)

1994

C)

1996

D)

1998

E)

2000

 

 

23.

When the polynomial is divided by , the remainder is .  Find .

 

 

A)

-4

B)

-2

C)

0

D)

2

E)

4

 

 

24.

A total of thirty natural numbers divide the number 1200 without remainder.  Express the product of these numbers in the form

 

 

A)

B)

C)

D)

E)

 

 

 

25.

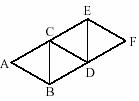
Four equilateral triangles each with side length 1 are arranged as shown below.  Find the distance from the point A to the point F.

 

 

 

A)

B)

C)

D)

E)

 

26.

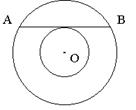
In the figure below, both circles are centered at the point O.  Moreover, the line segment AB is tangent to the smaller circle and has length 20 centimeters.  What is the area between the two circles?

 

 

A)

B)

C)

D)

E)

 

 

27.

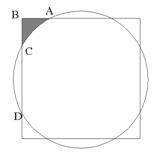
In the diagram, the circle and the square share the same center.  If the area of the shaded region , which is outside the circle and inside the square, equals the area of the region bounded by  and the minor arc , which is inside the circle and outside the square, compute the ratio of the side of the square to the radius of the circle.

 

 

A)

B)

C)

D)

E)

 

 

28.

Determine the sum of the three greatest consecutive integers each less than 200 for which the least number has 4 as a factor, the second number has 5 as a factor and the greatest number has 6 as a factor.

 

 

A)

200

B)

255

C)

375

D)

555

E)

575

 

 

29.

Tees.com advertises a limited-time sale, offering 1 shirt for $15 and two shirts for $25.  A total of 1250 shirts are sold for $16,750.  Determine the number of customers that ordered 2 shirts.

 

 

A)

200

B)

400

C)

625

D)

670

E)

850

 

 

30.

Determine the number of permutations of the letters in the word hippopotamus if all the letters are used without repetition.

 

 

A)

3,628,800

 

B)

39,916,800

 

C)

79,833,600

 

D)

159,667,200

 

E)

479,001,600
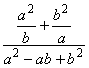