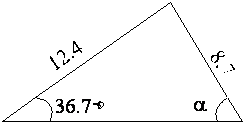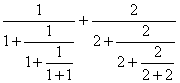High School Mathematics Contest Spring 2001

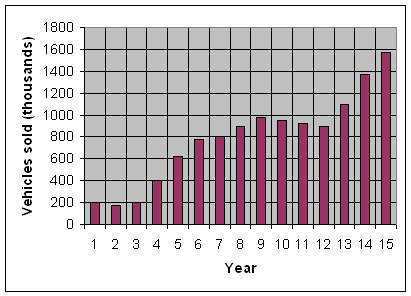
1.	The following bar graph shows the number of vehicles sold (in thousands) starting with Year 1 representing 1981. Determine the first year in which more than 1,000,000 vehicles were sold.
	A)	1990	B)	1991	C)	1992	D)	1993	E)	1994

2.	A league has 10 teams and every team plays each of the other teams exactly once. What is the total number of league games played?
	A)	10	B)	20	C)	45	D)	90	E)	100

3.	Given the arithmetic sequence 50, 54, 58, … How many terms must the sequence have for their mean to be 500?
	A)	200	B)	220	C)	224	D)	226	E)	250

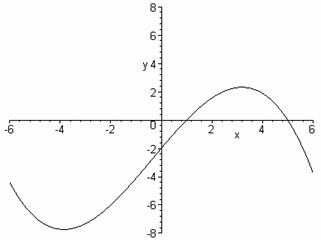
4.	Refer to the graph of f(x) below. Find f(f(f(1))).
	A)	-6	B)	-2	C)	0	D)	1	E)	3

5.

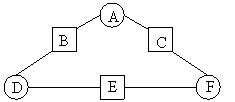
In the following diagram, each box contains the sum of the values in the circles directly linked to it. The values of the boxes are listed in the table. Determine the value in circle D.

Box	Value
B	203
C	497
E	-42

A)

-168

B)

-85

C)

126

D)

168

E)

252

6.	Which of the following are NOT consecutive terms in an arithmetic sequence?
	A)	2,2,2	B)	3,7,11	C)	2,4,8	D)	2,0,-2	E)

7.	A truncated cone has a top radius of 5 meters and a bottom radius of 8 meters. Its height is 4 meters. Determine the volume of the truncated cone in cubic meters. [The volume of a cone with height and radius is given by the formula ].
	A)		B)		C)		D)		E)

8.	In 1980 the world record for the 50m freestyle was set by Dara Torres at 25.96 seconds. In 2000 Inge de Bruijn set a new record at 24.39 seconds. At what rate (sec/yr) did the record improve?
	A)	.0314	B)	.0785	C)	.6369	D)	1.57	E)	12.74

9.	Let be a function such that for integer values of n. If determine the value of .
	A)	6	B)	7	C)	21	D)	28	E)	33

10.	A triangle has two known side lengths of 12.4 and 8.7. The angle opposite the side of length 8.7 is . Find the measure of the angle opposite the side of length 12.4.
	A)		B)		C)		D)		E)

11.	A randomly chosen mother has two children. When she is asked whether she has at least one boy, she replies that she does. If the likelihood of having a boy is equal to the likelihood of having a girl, what is the probability that both her children are boys?
	A)		B)		C)		D)		E)

12.	Given that and (in radians), determine .
	A)		B)		C)		D)		E)

13.	I just finished playing three marble games and have twenty-one marbles. In the first game, I lost half my marbles. In the second game, I won eleven times what I had at the end of the first game. In the third game, I won nine marbles. Find the number of marbles I had when I started playing.
	A)	1	B)	2	C)	3	D)	4	E)	6

14.	Determine which of the following figures has both rotational and reflectional symmetry.
	A)		B)		C)		D)		E)

15.	Which of the following numbers can be expressed as the sum of the squares of six odd integers?
	A)	1997	B)	1998	C)	1999	D)	2000	E)	2001

16.

A poll of 100 registered voters revealed the following facts about the sources from which they received their news:

65	-	television	27	-	television & internet
39	-	newspaper	20	-	television & newspaper
39	-	internet	9	-	newspaper & internet
6 - television, newspaper & internet

Determine how many people received news from only one of the three sources.

A)

39

B)

44

C)

49

D)

55

E)

65

17.	Six consecutive integers are written on a blackboard. When one of them is erased, the sum of the remaining five is 2001. Find the number which was erased.
	A)	391	B)	394	C)	398	D)	402	E)	406

18.	How many 3-digit numbers are there for which the sum of the digits is 7? (A 3-digit number is defined to be a number with the first digit non-zero).
	A)	27	B)	28	C)	29	D)	30	E)	31

19.	A drawer contains 2 red socks, 2 white socks, and 2 blue socks. If two socks are drawn at random from the drawer, what is the probability that they will form a matching pair?
	A)		B)		C)		D)		E)

20.	A square is divided into a 5 by 5 red-and-black checkerboard pattern, with the corner squares colored red. What percentage of the entire square is colored red?
	A)	40%	B)	48%	C)	50%	D)	52%	E)	55%

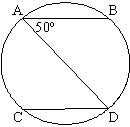
21.	In the circle below, and is a diameter of the circle. If, what is the number of inches in the length of the arc? Express your answer in terms of .
	A)		B)		C)		D)		E)

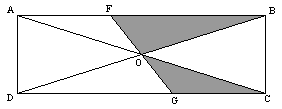
22.	In rectangle , and . , and are concurrent at point . What is the number of square centimeters in the area of the shaded region?
	A)	10	B)	15	C)	20	D)	35	E)	40

23.	Find the number of integer solutions of .
	A)	5	B)	6	C)	8	D)	10	E)	12

24.	Simplify given that is a positive real number.
	A)		B)		C)		D)		E)

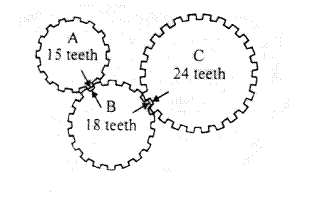
25.	Gears A, B and C are aligned as shown, and each gear has the number of teeth indicated. Determine the least positive number of rotations gear C must make before the arrows will again be aligned in the same way.
	A)	15	B)	18	C)	24	D)	90	E)	360

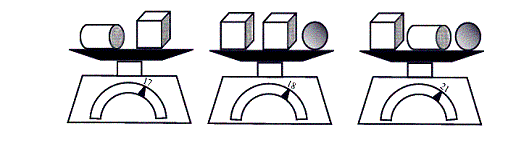
26.	The scales show the weights of different collections of cylinders, cubes and spheres. Weights given by the scales are in kilograms. One cylinder and one cube weigh 17 kg, two cubes and one sphere weigh 18 kg, and one cube, one cylinder and one sphere weigh 21 kg. Assuming that the same shapes have the same weight, what is the weight of a cylinder?
	A)	3	B)	4	C)	7	D)	9	E)	10

27.	At the Pizza Paradise, a pizza with a diameter costs $10. Given that the cost of a pizza is directly proportional to its area, determine the cost of a pizza with a diameter. Express your answer to the nearest cent.
	A)	$13.65	B)	$14.00	C)	$15.00	D)	$17.90	E)	$19.60

28.	Simplify and express your answer as a common fraction.
	A)		B)		C)		D)		E)	3

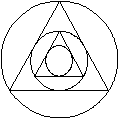
29.	The figure below consists of a large circle with successively smaller inscribed equilateral triangles and circles. The area of the smallest circle is square meters. Find how many square meters are in the area of the largest circle and express your answer in terms of .
	A)		B)		C)		D)		E)

30.	A rectangular solid is cut by slicing through the midpoints of three adjacent sides. Calculate the number of inches in the sum of the lengths of the edges of the resulting tetrahedron. Express your answer as a decimal rounded to the nearest tenth.
	A)	9	B)	9.2	C)	13.1	D)	19.7	E)	22.1