Fourier Analysis of Time Series
by Dr. R. L. Herman, UNC Wilmington
Friday, September 20, 2002
This is a work in
progress.
Introduction
Often one is interested in determining the frequency content of signals. Signals are typically represented as time dependent functions. Real signals are continuous, or analog signals. However, through sampling the signal by gathering data, the signal does not contain high frequencies and is finite in length. The data is then discrete and the corresponding frequencies are discrete and bounded. Thus, in the process of gathering data, one seriously affects the frequency content of the signal. This is true for simple a superposition of signals with fixed frequencies. The situation becomes more complicated if the data has an overall non-constant trend or even exists in the presence of noise.
From Transforms to Series
To be completed.
Fourier Series
As described in the last section (hopefully), we have seen
that by restricting our data to a time interval [0, T] for period T, and
extending the data to ![]() , one generates a periodic function of infinite duration at
the cost of losing data outside the fundamental range. This is not unphysical,
as the data is typically taken over a finite period of time. Thus, any physical
results in the analysis can be obtained be restricting the outcome to the given
period.
, one generates a periodic function of infinite duration at
the cost of losing data outside the fundamental range. This is not unphysical,
as the data is typically taken over a finite period of time. Thus, any physical
results in the analysis can be obtained be restricting the outcome to the given
period.
In typical problems one seeks a representation of the
signal, valid for ![]() as
as
![]()
where the angular frequency is given by
![]()
Note that f(t) is periodic with period P=T: ![]() Most signals have an
infinite period, so we already have made a first approximation. Thus, this has
restricted the physical data to
Most signals have an
infinite period, so we already have made a first approximation. Thus, this has
restricted the physical data to ![]() [That is, by limiting
t, we are forced to using discrete frequencies, or the above sum as
opposed to an integral in the Fourier Transform in the last section.]
[That is, by limiting
t, we are forced to using discrete frequencies, or the above sum as
opposed to an integral in the Fourier Transform in the last section.]
One can extract the Fourier Coefficients (![]() ) using the orthogonality of the trigonometric basis. Namely, such orthogonality for a set
) using the orthogonality of the trigonometric basis. Namely, such orthogonality for a set ![]() over the interval
over the interval ![]() with weight
with weight ![]() is given by the
condition
is given by the
condition ![]()
For the trigonometric functions, this is given by the relations
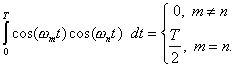
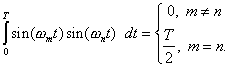
![]()
These relations are proved in Appendix A. The coefficients are found to in Appendix B as
![]()
![]()
Discrete Series
In the previous analysis we had restricted time to the interval [0,T], leading to a Fourier series with discrete frequencies and a periodic function of time. In reality, taking data can only be done at certain frequencies, thus eliminating high frequencies. Such a restriction on the frequency will lead to a discretization of the data in time. Another way to view this is that when recording data we sample at a finite number of time steps, limiting our ability to collect data with large oscillations. Thus, we not only have discrete frequencies but we also have discrete times.
This can be captured in the following representation:
![]()
where the time, time step and trigonometric arguments are given by
![]()
![]() and
and ![]()
We need to determine M and the unknown coefficients. As for
the Fourier series, we rely on an orthogonality principle, but this time
replacing the integral by a sum. Again we will determine the unknowns in terms
of the given samples of the function f(t). The orthogonality is provided
in Appendix C. If we take N samples, we can the determine N unknown
coefficients ![]() and
and ![]() Thus, we can fix
Thus, we can fix ![]() Often the
coefficients
Often the
coefficients ![]() and
and ![]() are included for symmetry. Note that the corresponding sine
function factors evaluate to zero, leaving these two coefficients arbitrary.
Thus, we can take them to be zero.
are included for symmetry. Note that the corresponding sine
function factors evaluate to zero, leaving these two coefficients arbitrary.
Thus, we can take them to be zero.
The full set of coefficients are found to be (in Appendix D)
![]()
![]()
![]()
![]()
![]()
Matlab Implementation
In this section we provide implementations
of the discrete trigonometric transform in Matlab. The first implementation is
a straightforward one which can be done in most programming languages. The
second implementation makes use of matrix computations that can be performed in
Matlab. Sums can be done with matrix multiplication, as describes in Appendix
I. This eliminates the loops in the program.
Direct Implementation without special use of matrix algebra
%
% DFT in a direct implementation
%
% Enter Data in y
y=[7.6 7.4 8.2 9.2 10.2 11.5 12.4 13.4 13.7 11.8
10.1 ...
9.0 8.9
9.5 10.6 11.4 12.9 12.7 13.9 14.2 13.5 11.4 10.9 8.1];
% Get length of data vector or number of samples
N=length(y);
% Compute Fourier Coefficients
for p=1:N/2+1
A(p)=0;
B(p)=0;
for n=1:N
A(p)=A(p)+2/N*y(n)*cos(2*pi*(p-1)*n/N)';
B(p)=B(p)+2/N*y(n)*sin(2*pi*(p-1)*n/N)';
end
end
A(N/2+1)=A(N/2+1)/2;
% Reconstruct Signal - pmax is number of frequencies
used in increasing order
pmax=13;
for n=1:N
ynew(n)=A(1)/2;
for
p=2:pmax
ynew(n)=ynew(n)+A(p)*cos(2*pi*(p-1)*n/N)+B(p)*sin(2*pi*(p-1)*n/N);
end
end
% Plot Data
plot(y,'o')
% Plot reconstruction over data
hold on
plot(ynew,'r')
hold off
Compact Implementation
This implementation uses matrix products and is described in Appendix H.
%
% DFT in a compact implementation
%
% Enter Data in y
y=[7.6 7.4 8.2 9.2 10.2 11.5 12.4 13.4 13.7 11.8
10.1 ...
9.0 8.9
9.5 10.6 11.4 12.9 12.7 13.9 14.2 13.5 11.4 10.9 8.1];
N=length(y);
% Compute the matrices of trigonometric functions
p=1:N/2+1;
n=1:N;
C=cos(2*pi*n'*(p-1)/N);
S=sin(2*pi*n'*(p-1)/N);
% Compute Fourier Coefficients
A=2/N*y*C;
B=2/N*y*S
A(N/2+1)=A(N/2+1)/2;
% Reconstruct Signal - pmax is number of frequencies
used in increasing order
pmax=13;
ynew=A(1)/2+C(:,2:pmax)*A(2:pmax)'+S(:,2:pmax)*B(2:pmax)';
% Plot Data
plot(y,'o')
% Plot reconstruction over data
hold on
plot(ynew,'r')
hold off
Appendices
A. Orthogonality of Trigonometric Basis
We want to prove the relations
(for ![]() ,
, ![]() )
)
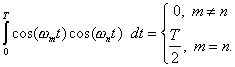
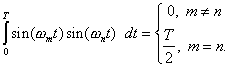
![]()
These are based upon the
trigonometric identities in Appendix F. For ![]()
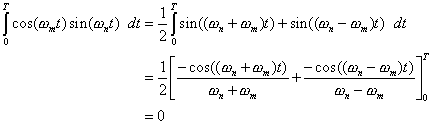
since ![]() and
and ![]() for n and m
integers. Similarly, the other integrals can be computed.
for n and m
integers. Similarly, the other integrals can be computed.
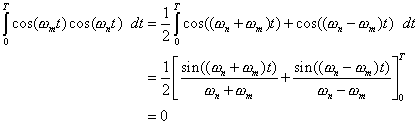
since ![]() Finally,
Finally,
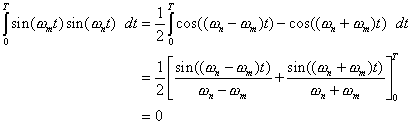
For ![]() we have instead
we have instead
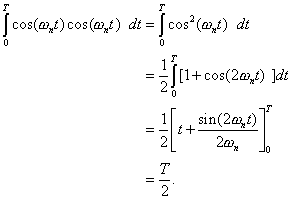
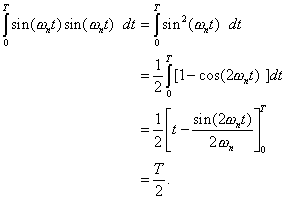
Here we have used the trigonometric identities ![]() and
and ![]() , which are obtainable from the identities in Appendix F.
, which are obtainable from the identities in Appendix F.
B. Derivation of Fourier Coefficients
We now look at the Fourier series representation
![]()
We can use the orthogonality relations in the last Appendix in order to arrive at expressions for the Fourier coefficients.
First, we integrate the series over one period.
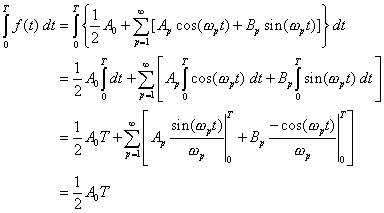
This will give the expression ![]()
Now multiply the series by ![]() for some
for some ![]() and integrate.
and integrate.
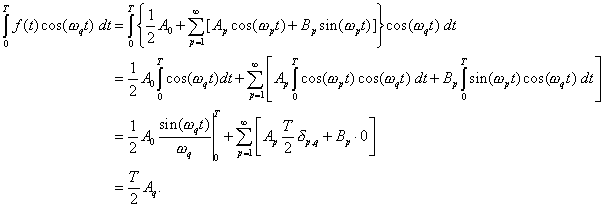
Here use was made of the known orthogonality relations from the last section. Also, the Kronecker delta was used, defined as
![]()
This renders the sum above a sum with all zero terms except
for one, that for ![]()
For example, if ![]() we have
we have
![]()
Thus, one can solve for the ![]() 's to obtain
's to obtain![]()
Similarly, one has
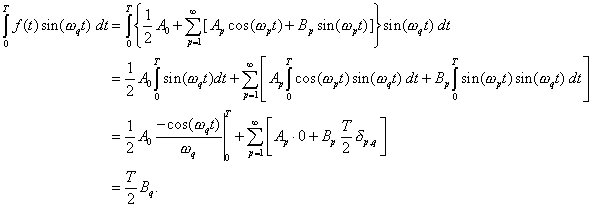 So,
So, ![]()
C. Discrete Orthogonality
The derivation of the discrete Fourier coefficients can be done using the discrete orthogonality of the discrete trigonometric basis similar to the derivation of the above Fourier coefficients for the Fourier series. We first prove the following
![]()
![]()
This can be done more easily using the exponential form,
![]()
by using Euler's formula, ![]() for each term in the
sum.
for each term in the
sum.
The exponential sum is the sum of a geometric progression, which can be summed as done in Appendix G. Thus, we have
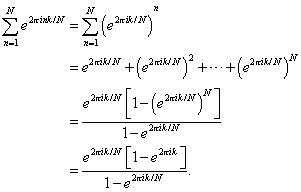
As long as ![]() the numerator is 0.
In the special cases that
the numerator is 0.
In the special cases that ![]() , we have
, we have ![]() So,
So,
![]()
Therefore,
![]() and the result
follows.
and the result
follows.
We can use this to establish
orthogonality relations of the following type for ![]() :
:
![]()
Splitting the above sum into two sums and then evaluating the separate sums from earlier in this section,
![]()
![]()
we obtain
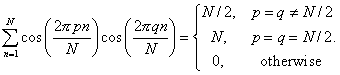
Similarly, we find
![]()
and
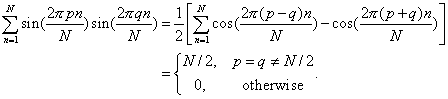
D. Discrete Transform
The derivation of the coefficients for the DFT is now easily obtained using the discrete orthogonality in the last section. We start with the expansion
![]()
We first sum over n:
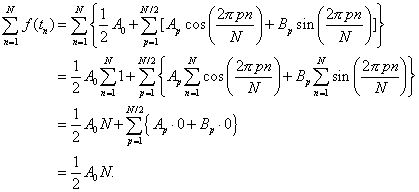
Now, we can multiply both sides of the expansion by ![]() and sum over n.
and sum over n.
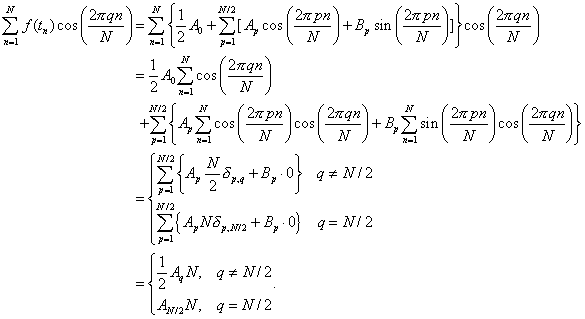 So, we have found that
So, we have found that
![]()
![]()
Similarly,
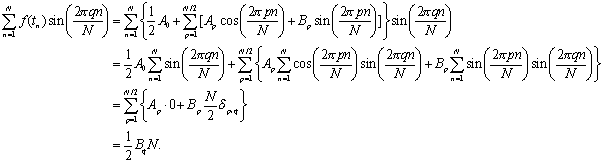 Finally, we have
Finally, we have
![]()
E. The Discrete Exponential Transform
The derivation of the coefficients for the DFT was obtained using the discrete orthogonality in the last section. However, this is not the form used in Matlab for spectral analysis. Matlab allows for the computation of the Fast Fourier Transform (FFT) and its description in the help section does not involve sines and cosines. Namely, Matlab defines the transform and inverse transform as
"For length N input vector x,
the DFT is a length N vector X, with elements
N
X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k
<= N.
n=1
The inverse DFT (computed by IFFT) is given by
N
x(n) = (1/N) sum
X(k)*exp( j*2*pi*(k-1)*(n-1)/N), 1 <= n <= N.
k=1
The relationship between the DFT and the Fourier coefficients a
and b in
N/2
x(n) = a0 + sum
a(k)*cos(2*pi*k*t(n)/(N*dt))+b(k)*sin(2*pi*k*t(n)/(N*dt))
k=1
is
a0 = X(1)/N, a(k) = 2*real(X(k+1))/N, b(k) =
-2*imag(X(k+1))/N,
where x is a length N discrete signal sampled at times t with
spacing dt."
Or, it also provides the following:
![]()
![]() where
where ![]() for
for ![]()
In this section we will derive the discrete Fourier exponential transform in preparation for a discussion of FFT in the next section. We will start with the DFT.
![]()
Again, we can employ Euler's formula to rewrite the
trigonometric functions in terms of exponentials, Namely, using ![]() we have that
we have that
![]()
![]()
Then we have
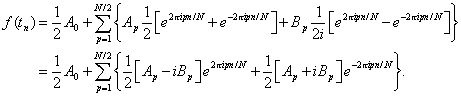
We define ![]() and note that the
above result can be written as
and note that the
above result can be written as
![]()
Here we have introduce the complex conjugate operation ![]()
The terms in the sums look similar. We can actually combine
them into one form. Note that ![]() Thus, we can write
Thus, we can write
![]() in the second sum.
Since
in the second sum.
Since ![]() , we see that
, we see that ![]() So, we can rewrite
the second sum as
So, we can rewrite
the second sum as
![]()
Since q is a dummy index (it can be replaced by any letter without changing the value of the sum), we can replace it with a p and combine the terms in both sums to obtain
![]()
where
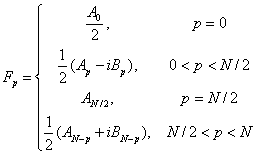
Notice that the real and imaginary parts of the Fourier
coefficients obey certain symmetry properties over the full range of the
indices since the real and imaginary parts are related between ![]() and
and ![]() [A description of
this will be provided later.]
[A description of
this will be provided later.]
We can know determine the coefficients in terms of the sampled data.
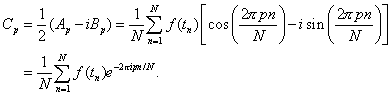
Thus,
![]()
and
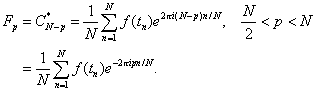
We have shown that for all F's but two, the form is
![]()
However, we can easilty show that this is also true when ![]() and
and ![]()
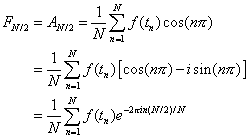
and
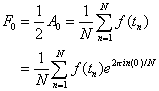
Thus, all of the ![]() 's are of the same form. This gives us the discrete transform
pair
's are of the same form. This gives us the discrete transform
pair
![]()
![]() .
.
Note that this is similar to the definition of the FFT given in Matlab.
F. Fast Fourier Transform
The usual computation of the discrete Fourier transform is
done using the Fast Fouier Transform (FFT). There are various implementations
of it, but a standard form is the Radix-2 FFT. We describe this FFT in the
current section. We begin by writing the DFT compactly using ![]() . Note that
. Note that ![]() and
and ![]() We can then write
We can then write
![]()
The key to the FFT is that this sum can be written as two similar sums:
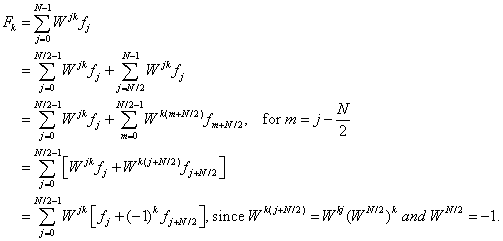
Thus, the sum appears to be of the same form as before, but
there are half as many terms with a different coefficient for the ![]() 's. In fact, we can separate the terms involving the + or –
sign by looking at the even and odd values of k.
's. In fact, we can separate the terms involving the + or –
sign by looking at the even and odd values of k.
For even ![]() we have
we have
![]()
For odd ![]() we have
we have
![]()
Each of these equations gives the Fourier coefficients in
terms of a similar sum using fewer terms and with a different weight, ![]() IF N is a
power of 2, then this process can be repeated over and over until one ends up
with a simple sum.
IF N is a
power of 2, then this process can be repeated over and over until one ends up
with a simple sum.
The process is easily seen when written out for a small
number of samples. Let ![]() Then a first pass at
the above gives
Then a first pass at
the above gives
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The point is that the terms in these expressions can be
regrouped with ![]() and noting
and noting ![]() :
:
![]()
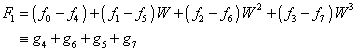
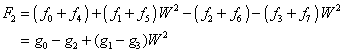
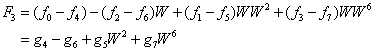
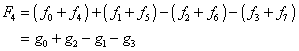
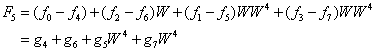
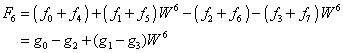
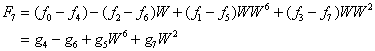
However, each of the g-series can be rewritten as well, leading to
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus, the computation of the Fourier coefficients amounts to
inputting the f's and computing the g's. This takes 8 additions
and 4 multiplications. Then one get the h's, which is another 8
additions and 4 multiplications. There are three stages, amounting to a total
of 12 multiplications and 24 additions. Carrying out the process in general,
one has ![]() steps with
steps with ![]() multiplications and N
additions per step. In the direct computation one has
multiplications and N
additions per step. In the direct computation one has ![]() multiplications and
multiplications and ![]() additions. Thus, for
additions. Thus, for ![]() that would be 49
multiplications and 56 additions.
that would be 49
multiplications and 56 additions.
The above process is typically shown schematically in a "butterfly diagram". Examples can be found at other sites. One might be provided here at a later date. For now, we have the basic butterfly transformation displayed as
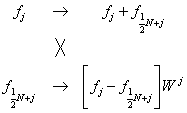
In the actual implementation, one computes with the h's in the following order:
|
Output and Binary Representation |
Desired Order |
|
|
|
The binary representation of the index was also listed. Notice that the output is in bit-reversed order as compared to the right side of the table which shows the coefficients in the correct order. [Just compare the columns in each set of binary representations.] So, typically there is a bit reversal routine needed to unscramble the order of the output coefficients in order to use them.
G. Trigonometric Identities
The basic trigonometric identities that one needs the product of trigonometric functions expanded as simple expressions. These are based upon the sum and difference identities:
![]()
![]() .
.
Adding or subtracting one obtains
![]()
![]()
![]() .
.
H. Geometric Progression
Another frequently occurring
computation is the sum of a geometric progression. This is a sum of the form ![]() . This is a sum of
. This is a sum of ![]() terms in which
consecutive terms have a constant ratio,
terms in which
consecutive terms have a constant ratio, ![]() The sum is easily
computed. One multiplies the sum
The sum is easily
computed. One multiplies the sum ![]() by
by ![]() and subtracts the
resulting sum from the original sum to obtain
and subtracts the
resulting sum from the original sum to obtain
![]()
Factoring on both sides of this chain of equations yields the desired sum,
![]()
I. Matrix Operations for Matlab
The beauty of using Matlab is that many operations can be performed using matrix operations and that one can perform complex arithmetic. This eliminates many loops and make the coding of computations quicker. However, one needs to be able to understand the formalism. In this section we elaborate on these operations so that one can see how the Matlab implementation of the direct computation of the DFT can be carried out in compact form as shown previously in the Matlab Implementation section. This is all based upon the structure of Matlab, which is essentially a MATrix LABoratory.
A key operation between matrices is matrix multiplication.
An ![]() matrix is simply a
collection of numbers arranged in n rows and m columns. For
example, the matrix
matrix is simply a
collection of numbers arranged in n rows and m columns. For
example, the matrix
![]() is a
is a ![]() matrix. The entries
(elements) of a general matrix A can be represented as
matrix. The entries
(elements) of a general matrix A can be represented as ![]() which represents the ith row and jth column.
which represents the ith row and jth column.
Given two matrices, A and B, we can define the
multiplication of these matrices when the number of columns of A equals
the number of rows of B. The product, which we represent as matrix C,
is given by the ijth element of C. In particular, we let A
be a![]() matrix and B an
matrix and B an ![]() matrix. The product, C,
will be a
matrix. The product, C,
will be a ![]() matrix with entries
matrix with entries
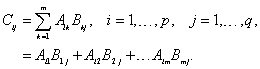
If we wanted to compute the sum ![]() , then in a typical programming language we could use a loop,
such as
, then in a typical programming language we could use a loop,
such as
Sum =0
Loop n from 1 to N
Sum = Sum + a(n)*b(n)
End Loop
In Matlab we could do this with a loop as
above, or we could resort to matrix multiplication. We can let a and b be 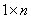 and
and 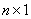 matrices,
respectively. Then the product would be a
matrices,
respectively. Then the product would be a 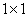 matrix; namely, the
sum we are seeking. However, these matrices are not always of the suggested
size.
matrix; namely, the
sum we are seeking. However, these matrices are not always of the suggested
size.
A ![]() matrix is called
a row vector and a
matrix is called
a row vector and a ![]() matrix is called
a column vector. Often we have that both are of the same type. One can convert
a row vector into a column vector, or vice versa, using the matrix operation
called a transpose. More generally, the transpose of a matrix is defined
as follows:
matrix is called
a column vector. Often we have that both are of the same type. One can convert
a row vector into a column vector, or vice versa, using the matrix operation
called a transpose. More generally, the transpose of a matrix is defined
as follows: ![]() has the elements
satisfying
has the elements
satisfying ![]() .
.
In Matlab, the transpose if a matrix A is ![]() .
.
Thus, if we want to perform the above sum, we have ![]() . In particular, if both a and b are row
vectors, the sum in Matlab is given by
. In particular, if both a and b are row
vectors, the sum in Matlab is given by ![]() and if they are both
row vectors, the sum is
and if they are both
row vectors, the sum is ![]() This notation is much
easier to type.
This notation is much
easier to type.
In our computation of the DFT, we have many sums. For example, we want to compute the coefficients of the sine functions,
![]()
The sum can be computed as a matrix product. The function y
only has values at times ![]() This is the sampled
data. We can represent it as a vector. The sine functions take values at
arguments (angles) depending upon p and n. So, we can represent
the sines as an
This is the sampled
data. We can represent it as a vector. The sine functions take values at
arguments (angles) depending upon p and n. So, we can represent
the sines as an ![]() or
or ![]() matrix. The Fourier
coefficient thus becomes a simple matrix multiplication, ignoring the prefactor
matrix. The Fourier
coefficient thus becomes a simple matrix multiplication, ignoring the prefactor
![]() . Thus, if we put the sampled data in a
. Thus, if we put the sampled data in a ![]() vector Y and
put the sines in an
vector Y and
put the sines in an ![]() vector S, the
Fourier coefficient will be the product, which has size
vector S, the
Fourier coefficient will be the product, which has size ![]() . Thus, in the code we see that these coefficients are
computed as B=2/N*y*S for the given y and B matrices. The A coefficients are computed in the same
manner. Comparing the two codes in that section, we see how much easier it is
to implement. However, the number of multiplications and additions has not
decreased. This is why the FFT is generally better. But, seeing the direct
implementation helps one to understand what is being computed before seeking a
more efficient implementation, such as the FFT.
. Thus, in the code we see that these coefficients are
computed as B=2/N*y*S for the given y and B matrices. The A coefficients are computed in the same
manner. Comparing the two codes in that section, we see how much easier it is
to implement. However, the number of multiplications and additions has not
decreased. This is why the FFT is generally better. But, seeing the direct
implementation helps one to understand what is being computed before seeking a
more efficient implementation, such as the FFT.