Course Syllabus

Back

Syllabus - PDF

Course Content:  

Required Text: An Introduction to Fourier Analysis, R. Herman, CRC Press, 2016.

Optional Materials: Additional readings are posted at the course web site. These include references to several online lecture notes and applets. The course site is http://people.uncw.edu/hermanr/mat367.

In this class we will cover a variety of topics in analysis and their applications. These will include infinite series, power series, uniform convergence, Fourier series, orthogonal polynomials, special functions, integral transforms, complex variables and residue theory. We will tie these topics together by the analysis of analog signals and digital signals.

Course Goals:

After completing this course, students should be familiar with

• Convergence and summation of infinite series.
• Representation, or approximation, of functions by series representations.
• Legendre, Bessel, gamma, and delta functions.
• Fourier (trigonometric, Legendre, Bessel, polynomial) series.
• Complex numbers and functions.
• Analytic functions and integration in the complex plane.
• Integral transforms and their applications.
• Relationship between analog and digital signals.

Course Philosophy:

"Applied mathematics should read like a good mystery, with an intriguing beginning, a clever but systematic middle, and a satisfying resolution at the end. Often, however, the resolution of one mystery opens up a whole new problem, and the process starts all over. For the applied mathematical scientist, there is the goal to explain or predict the behavior of some physical situation. One begins by constructing a mathematical model which captures the essential features of the problem without masking its content with overwhelming detail. Then comes the analysis of the model where every possible tool is tried, and some new tools developed, in order to understand the behavior of the models as thoroughly as possible. Finally, one must interpret and compare these results with real world facts. Sometimes this comparison is quite satisfactory, but most often one discovers that important features of the problem are not adequately accounted for, and the process begins again." - James P. Keener, Principles of Applied Mathematics.

In fact, there are many tools that have been discovered over the last couple of centuries for solving problems in a variety of disciplines. Many of these have come from the study of partial differential equations, but can also be developed outside of this field. We will look at this course as the beginning of a long process towards the understanding of some of the most fundamental tools in applied mathematics. We will begin to sense the deep connections between several areas of mathematics, such as real and complex analysis, linear algebra, differential equations, and modern algebra.

The main theme running throughout the course is to look at representations of functions as a sum over some basis functions, which can be written as 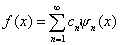 , or 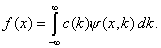We are then faced with three problems:

1) What are good basis functions?
2) How do we find the expansion coefficients, c?
3) Do these "sums" converge to the functions they are supposed to represent?

We will begin with the study of the representation of functions as power series and trigonometric, or Fourier, series. It was the introduction and study of the convergence of these infinite series that lead to deep results in analysis. We can then generalize these to expansions over other functions, as the beginning of an understanding that the psi functions can be viewed as a set of basis vectors (in some cases, these are called harmonics) in an infinite dimensional space.

This is precisely the background needed to understand spectral analysis. However, no matter how hard we try, in real applications continuous signals are measured and discretized and the relationship between the continuous sums (integrals) and discrete sums (series expansions) has to be understood in order to make sense out of any spectral analysis. This theme of signal analysis and reconstruction from its spectral content will permeate the course.

Finally, in order to fully appreciate Fourier transforms, we will need to understand how various software packages implement these transforms and to see what errors are typically present. So, you will be exposed to some elementary programming in MATLAB and Maple. Numerical computation is another tool, which is very important nowadays for scientists.

Course Requirements:

Attendence: YOU ARE EXPECTED TO ATTEND ALL OF THE LECTURES! After three excused absences, there will be a penalty of 2% for each absence from your total grade.

Homework: Homework assignments will be collected on a regular basis and you will be told when the work is due. As doing homework is very important for learning the material in this course, it will count as 30% of your grade.

Computer Work: Technology is one of the most important tools in studying applied mathematics. You will be exposed to more advanced techniques of using the software we have around campus. This will include Maple, MATLAB, web applets and other applications. Besides using these tools in homework, you will have a project to do. This will count 10% of your grade.

Exams and Grades: There will be three exams and a final. The exams will cover the basic material up to the date of the exam. The tentative dates for the exams are below. 

Your final grade will be based on the following:

Plus-minus grading may be used in special cases.