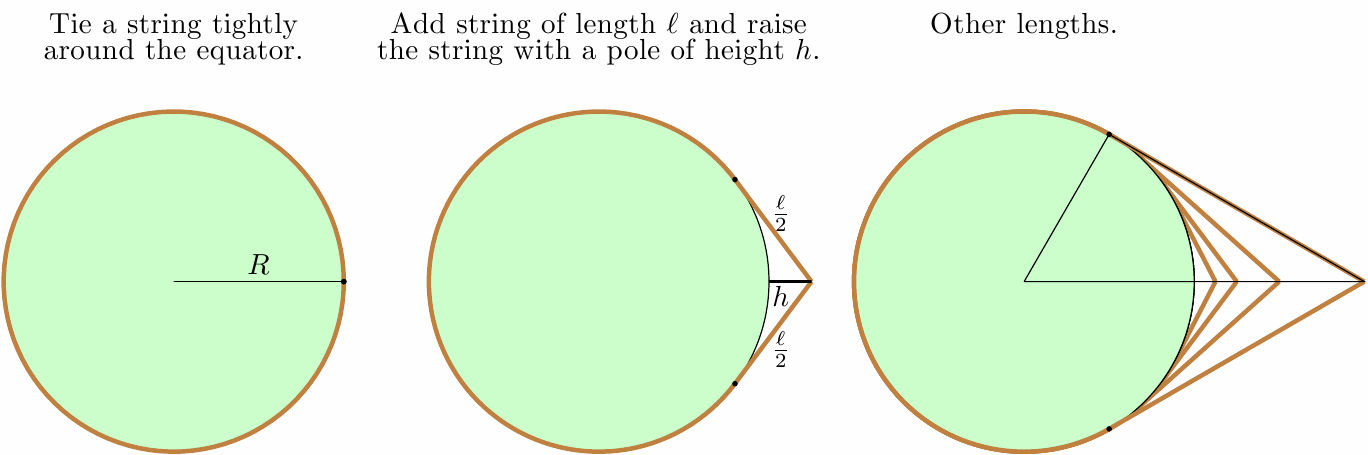
Problem
Tie a string around the
Earth’s equator so that it is tight. Now, add ten feet to the string. Pull
it at one point until it is tight but comes up to a point. How far from the
Earth’s surface is this? (i.e., how long a pole would you need to support the
rope)
-
Everyone needs to be in a group. (By Friday, 2/17).
-
Make an intelligent guess. Members of the class had guessed 5 ft or 10
ft.
-
Working with your partner, determine from the geometry a set of
equations to be solved for h given R and l. Everyone
will use the radius of the Earth as 21008452.488 ft. Write up and turn in
on Wednesday 2/23.
-
After you have turned
in your equations, I will provide you with a uniform set of equations
and instructions for the next part of the project. In the end you will
write up a group report with an analysis of how you solved the equations
and a justification for the digits that you report such as reporting the
computed relative error based on things like floating point
computations.
-
The
next set of instructions will be posted after 2/23.
To how many digits can
we
give and answer? Can you defend the number of digits in your answer?
Top
|
