PSY 555 Homework 5
Answers
3.8. Diagnostically meaningful cutoff:
Z
Score Area above Z
1.2800 .1003
1.2817 .1000
1.2900 .0985
z=![]()
-1.2817=![]()
111.549=![]()
The
diagnostically meaningful cutoff would be 112.
3.9(a).
Next
year's salary raises:
Z=![]()
-1.2817=![]()
X=$2512.68
So
the most productive 10% of the faculty will have a raise equal to or greater
than $2512.68.
3.9(b).
z=![]()
-1.645=![]()
X=$1342
The
5% of the faculty who haven't done anything useful in years will receive no
more than $1342 each and probably don't deserve that much.
3.10(a).
3.10(b).
z=![]() =
=![]()
A
count this high (or higher) would occur by chance only .5% of the time. Thus, there is definite reason to suspect
that this count has been fabricated by the student.
3.11. Transforming
scores on a diagnostic test for language problems:
X1=original
scores m1=48 s1=7
X2=transformed
scores m2=80 s2=10
s2=s1/C
10=7/C
C=.7
Therefore,
to transform the original standard deviation from 7 to 10, we need to divide
the original scores by .7. However,
dividing the original scores by .7 divides their mean by .7.
![]()
We
want to raise the mean to 80.80-68.57=11.43.
Therefore, we need to add 11.43 to each score.
X2=
X1/.07+11.43 [This formula summarizes the whole process].
3.13. October 1981
GRES, all people taking exam:
z=![]()
z=![]()
p(larger portion)=.81
A
GRE score of 600 would correspond to the 81st percentile.
3.14. For the data
in Exercise 3.13:
z=![]()
.6754=![]()
X=573.987
Z
Score P
.6700 .7486
.6745 .7500
.6800 .7517
A
GRE score of (.6745*126+489)=574 would correspond to the 75th
percentile.
3.15. October 1981
GRE, all seniors and nonenrolled college graduates.
z=![]() z=
z=![]()
z=![]() .6745=
.6745=![]()
p=.785 X=586.591
3.18. Diagnostically
meaningful cutoff for the Behavior Problem scores:
z=![]()
.6745=![]()
X=cutoff=70.54
Z
Score P
2.050 .9798
2.054 .9800
2.060 .9803
1. A.
We assume that many variables are normally distributed in the
population, so the
normal
distribution is a good approximation of the population distribution.
B. Assumption of normality allows us to use
tools to draw inferences about variable values.
C. If we drew the distribution of the sample
means of many different samples, it would theoretically be a normal
distribution (i.e., the sampling distribution of the means would be a normal
distribution).
D. Most statistical tests that are commonly used
assume a normal distribution.
(See
p. 76 in the book for elaboration)
2(a). z=![]()
z=.25![]() .0987
.0987
z=.50![]() .1915
.1915
.1915-.0987=.0928
9.28%
of the distribution will fall between z-scores of .25 and .50.
2(b). z=![]()
z=-1.5![]() .4332
.4332
z=.5![]() .1915
.1915
.4332+.1915=.6247
62.47%
of the distribution will fall between z-scores of -1.5 and .5.
2(c). z=![]()
z=1.5![]() .4332
.4332
43.32%
of the distribution will fall between z-scores of 0 and 1.5.
2(d). z=![]()
z=.50![]() .1915
.1915
z=1.75![]() .4599
.4599
.4599-.1915=.2684
26.84%
of the distribution will fall between z-scores of .50 and 1.75.
3(a). ![]()
The
value of X is 38.92.
3(b). ![]()
The
value of ![]() is 19.05.
is 19.05.
3(c). z=![]()
![]()
The
value of ![]() is 18.31.
is 18.31.
4. ![]()
![]()
![]()
z=![]()
z=![]()
z=-.5![]() .1915+.5=.6915
.1915+.5=.6915
The
probability/likelihood that John will be late to his
5.
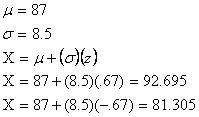
The
cutoff scores for assigning students to the three math courses should be 81.305
and 92.695.