PSY 555 Homework 4
Answers
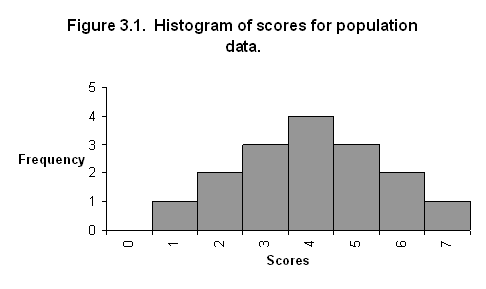
3.1(a). Original data:
1
2 2 3 3 3 4 4 4 4 5 5 5 6 6 7
or
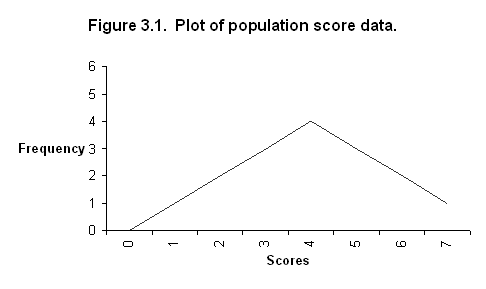
3.1(b). To convert the distribution to a
distribution of X-m, subtract m=4 from each score.
-3
-2 -2 -1 -1 -1 0 0 0 0 1 1 1 2 2 3
3.1(c). To complete the conversion to z, divide each
score by s=1.63:
-1.84
-1.23 -1.23 -.61 -.61 -.61 0 0 0 0 .61 .61 .61 1.23 1.23 1.84
3.2. Converting specific scores from the
distribution in Exercise 3.1 into z scores.
Z=
Z=-.92=+1.35=+3.07
Score
(X) Z Score
2.5 -.92 18%of
the distribution lies below X=2.5
6.2 +1.35 91%
of the distribution lies below X=6.2
9.0 +3.07 99.9%
of the distribution lies below X=9.0
3.3(a). Errors counting shoppers in a major
department store:
z=
z=
Between +1 and m lie .3413
z=
Between -1 and m lie .3413
.3413+.3413=.6826
Therefore
between 960 and 990 are found approximately 68% of the scores.
3.3(b). 975=m; therefore, 50% of the scores lie below 975.
3.3(c). .5000 lie below 975
.3413
lie between 975 and 990
.8413
(or 84%) lie below 990.
3.4(a). Using the data in Exercise 3.3, from
Appendix Z:
Z
Score Area between Z and Mean
.67 .2486
.6745 .2500 [interpolation
from Appendix Z]
.68 .2517
Therefore,
z=
.6745 encompasses the middle 50%.
z=
.6745=
X=958.12
and 964.88
50%
of the scores lie between counts of 965 and 985.
3.4(b).
75% of the counts would be less than 985 because we just calculated the
middle 50%, 25% of which lie on either side of the mean. Since 50% lie below the mean, 50+25=75% lie below
985.
3.4(c). What scores would 95% of the counts lie
between?
z=
.6745=
945.6 and 1004.4
95%
of the counts would lie between 946 and 1004.
3.6(a).
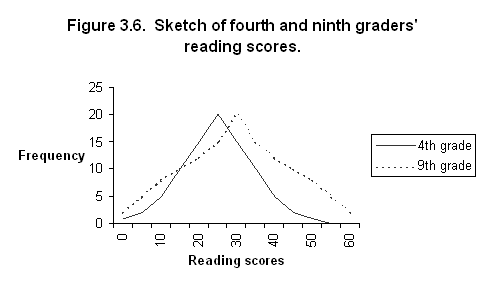
3.6(b). z=
The
smaller portion for z=1.00 is .1587.
Therefore 16% of the 4th graders score better than the
average 9th grader.
3.6(c). z=
The
smaller portion of the 9th graders score worse than the average 4th
grader.
1(a).
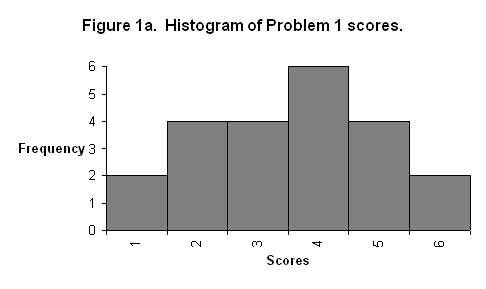
1(b).
|
X |
Freq |
Cum Freq |
Cum % |
|
6 |
2 |
22 |
100% |
|
5 |
4 |
20 |
91% |
|
4 |
6 |
16 |
73% |
|
3 |
4 |
10 |
45% |
|
2 |
4 |
6 |
27% |
|
1 |
2 |
2 |
9% |
The 45th percentile is 4.
1(c). 4.31 is the 70th percentile
(convert to a z).
1(d). 5 is the 73% percentile.
1(e). 5 is the minimum score needed to be in the
top 25% of the distribution.
1(f). Yes.
The distribution is fairly normal.
2. m=80
s=20
|
X |
Calculations and
Z-score |
|
85 |
Z= |
|
100 |
Z= |
|
120 |
Z= |
|
75 |
Z= |
|
65 |
Z= |
|
60 |
Z= |
|
130 |
Z= |
|
82 |
Z= |
|
68 |
Z= |
|
80 |
Z= |
|
105 |
Z= |
|
30 |
Z= |
3.
|
X |
(X-m)2 |
Z-score |
|
13 |
56.25 |
Z= |
|
17 |
12.25 |
Z= |
|
21 |
.25 |
Z= |
|
15 |
30.25 |
Z= |
|
16 |
20.25 |
Z= |
|
31 |
110.25 |
Z= |
|
23 |
6.25 |
Z= |
|
14 |
42.25 |
Z= |
|
27 |
42.25 |
Z= |
|
28 |
56.25 |
Z= |
m=
4.
m=85
X=72
Z=-1.0
Z
sZ=
Standard Deviation Calculation Problem
Answers
1.
|
X |
(X- |
|
13 |
139.24 |
|
21 |
14.44 |
|
27 |
4.84 |
|
31 |
38.44 |
|
35 |
104.04 |
|
24 |
.64 |
|
28 |
10.24 |
|
32 |
51.84 |
|
17 |
60.84 |
|
20 |
23.04 |
)2
2.
|
X |
(X- |
|
100 |
4.41 |
|
115 |
166.41 |
|
112 |
98.01 |
|
113 |
118.81 |
|
95 |
50.41 |
|
87 |
228.01 |
|
90 |
146.41 |
|
104 |
3.61 |
|
107 |
24.01 |
|
98 |
16.81 |
3.
|
X |
(X- |
|
55 |
0 |
|
54 |
1 |
|
59 |
16 |
|
55 |
0 |
|
52 |
9 |
|
51 |
16 |
|
57 |
4 |
|
49 |
36 |
|
61 |
36 |
|
57 |
4 |
