PSY 555 Homework 2
ANSWERS
2.2.
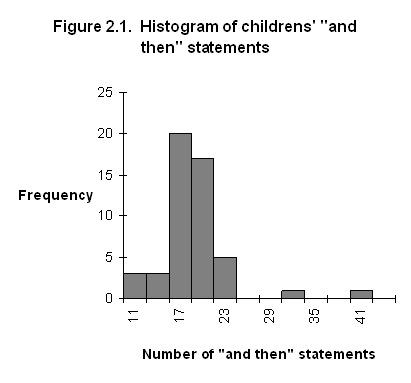
Children's "and then"
statements
Interval Midpoint
Frequency
10-12 11 3
13-15 14 3
16-18 17 20
19-21 20 17
22-24 23 5
25-27 26
0
28-30 29 0
31-33 32 1
34-36 35 0
37-39 38 0
40-42 41 1
2.4(a). The
scores for adults appear to be noticeably smaller. Adults seem to rely less strongly
than do children on an "and then…" format for recalling stories.
2.4(b).
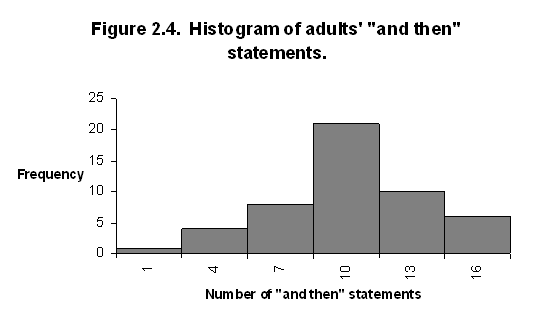
Adults' "and then"
statements
Interval Midpoint Frequency
0-2 1 1
3-5 4 4
6-8 7 8
9-11 10 21
12-14 13 10
15-17 16 6
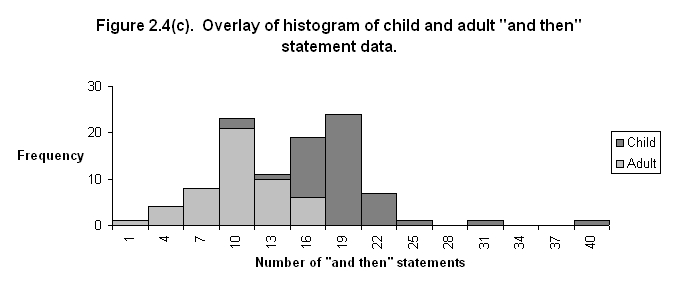
2.4(c).
Overlay the two histograms (from problems 2.2 and 2.4(b)) into one
histogram, using appropriate shading to indicate separate child and adult data,
as well as overlap between the two.
2.7.
Cumulative frequency
distribution for Exercise 2.4.
Adult Scores Frequency Cum. Frequency
1 1 1
3 1 2
4 1 3
5 2 5
7 4 9
8 4 13
9 7 20
10 8 28
11 6 34
12 5 39
13 1 40
14 4 44
15 3 47
16 2 49
17 1 50
2.14.
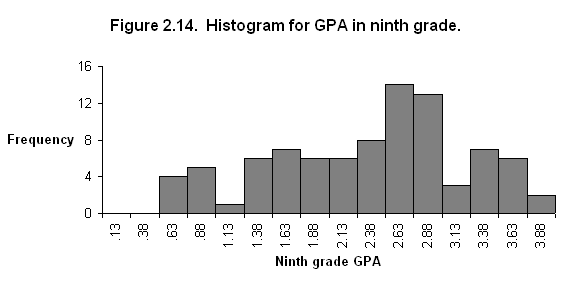
Histogram for GPA
GPA Interval Midpoint Frequency
.51-.75 .63 4
.76-1.00 .88 5
1.01-1.25 1.13 1
1.26-1.50 1.38 6
1.51-1.75 1.63 7
1.76-2.00 1.88 6
2.01-2.25 2.13 6
2.26-2.50 2.38 8
2.51-2.75 2.63 14
2.76-3.00 2.88 13
3.01-3.25 3.13 3
3.26-3.50 3.38 7
3.51-3.75 3.63 6
3.76-4.00 3.88 2
2.15.
Stem-and-leaf for ADDSC
Stem | Leaf
2. | 69
3* | 0344
3. | 56679
4* | 00023344444
4. | 5566677888899999
5* | 00000000011223334
5. | 55677889
6* | 00012234
6. | 55556899
7* | 0024
7. | 568
8* |
8. | 55
1. Problem
2.4: the mean is 10.2, the median is 10, and the mode is 10.
![]()
![]()
Median location=![]()
Median=![]()
Mode=10
(this score appears 8 times)
Problem
2.14: the mean is 2.46, the
median is 2.64, and the mode is 3
![]()
![]()
Median location=![]()
Median=![]()
Mode=3
(this score appears 13 times)
Problem
2.15: the mean is 52.6, the
median is 50, and the mode is 50.
![]()
Median location=![]()
Median=![]()
Mode=50 (this score appears 9 times)
2. The
distribution in 2.4 is unimodal with a very slight negative skew. The distribution in 2.14 is unimodal with a
negative skew. The distribution in 2.15
appears to be a normal (Gaussian) distribution.
3. A distribution must be symmetric and unimodal
in order for all three measure of central tendency to be the same value. The median is preferred over the mean when
there are outliers (because the mean will be unduly affected by extreme scores)
or when you are using an ordinal scale of measurement.
4. When there are observations that can assume
many different values (such as when you are using a continuous measurement
scale), it is not practical to include each individual value between the
endpoints of a scale in a frequency distribution because each value may only
appear once, if at all. So, instead, we
group adjacent values into intervals and then we list frequencies of each
interval to create a grouped frequency distribution (or histogram). Doing so summarizes the data and,
importantly, reduces noise.