PSY 555 Homework 19
Answers
1.
ANOVAs
and regression analyses are not really different procedures. In fact, ANOVA is a special case of
regression. Both analyses utilize the
F-distribution. ANOVA and regression
examine similar factors in the data (e.g., variances and standard errors) and
synthesize the relations between these factors in a statistical result. ANOVAs are calculated using a mathematical
simplification of regression analyses and are less powerful than regression
analyses. Thus, ANOVAs are generally
conducted when a regression is not appropriate (e.g., when portions along the
continuum of the X independent/predictor variable have not been observed and
assessed). In the past, ANOVAs were
commonly used because regression analyses are complex mathematically and so
they were difficult to calculate by hand (this factor was a weakness of
regression analyses in the past—this is not an issue anymore because of
statistical computer programs that complete these calculations easily). Both are examples of a general linear
model. The difference between ANOVA and
regression analyses is largely a matter of what can be concluded from the
results of these analyses. ANOVAs
determine whether different groups, or treatments, have different means, while
multiple regressions tell us how and if a mean is related to the treatments of
inclusions (of predictors) in a group.
2.
A t-test
compares the means of two groups in order to determine if the means are
significantly different. With only two
groups, we can easily conclude, if the means are different, which group has
higher or lower scores on a measurement.
An ANOVA also allows us to compare means and determine whether there are
significant differences among them, but is conducted when there are more than
two means (groups/treatments; a t-test between independent groups is actually
an ANOVA). ANOVAs also allow for using
more than one independent variable to be examined and determine the effect of
individual variables, as well as interactions among variables.
3.
The assumptions
underlying regression are similar to those of regression. These assumptions include homogeneity of
variance, normality of the distributions, and the independence of observations. The homogeneity of variance assumption refers
to the fact that ANOVA assumes each of our samples (treatments/conditions) has
approximately the same variance. The
normality assumption refers to the fact that we assume the dependent variable
(in the book the example was recall scores) is normally distributed for each of
our treatments/conditions. Finally, in
ANOVAs, we assume that observations are independent of one another—that is,
that is we know how one observation in an experimental condition stands
relative to that condition’s mean, it tells us nothing about the other
observation.
4.
The
three sources of variation for simple ANOVAs are the total variation, the error
variation, and the treatment variation.
The total variation (SSTOT) allows you to determine how much
the dependent variable observations deviate from the dependent variable mean
(across all observations)—essentially the amount of variation in the dependent
variable. The error variation, SSERR,
reflects the amount of variation that treatments do not explain. The treatment variation, SSTREAT,
tells us how much total variation treatments account for.
5.
![]()
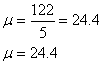
N=50
per group
|
|
|
|
|
21 |
-3.4 |
11.56 |
|
23 |
-1.4 |
1.96 |
|
27 |
2.6 |
6.76 |
|
22 |
-2.4 |
5.76 |
|
29 |
4.6 |
21.16 |
![]()
![]() N=5 2
N=5 2
N=5
S![]() =
=![]()
![]()
![]()
The best estimate of the population variance
is 591.68.