PSY 555 Homework 17
Answers
Chapter 15: #6,8,16,21
15.6. 
The
adjusted 
value is .2810.
15.8. The
regression coefficient of a variable indicates the slope of the best fit line
for the data. If a variable is collinear
with other predictors, then the slope will be changed dramatically based on the
other predictors that are used in the model (because their values will change
from sample to sample and the one variable’s observation points will covary
with the other predictor’s observations and the best fit line describing the
one variable’s data will change and so will the slope). If a variable is largely unrelated with the
other predictors, we would expect that the regression coefficient (slope) of
that variable would be relatively stable because only the random error from its
observations will influence its slope (rather than also having the other
variables’ random error influence its points and thus the model (and thus its
slope as well). In this case, the
inclusion of other variables in the model and thus their error would not
significantly alter the one variable and its parameter estimates. Thus, the stability of any regression
coefficient of a variable across different samples of data is partly a function
of how that variable relates with other predictors.
15.16(a). The
values of R for the successive steps are .6215, .7748, and .8181 (in successive
order).
15.16(b). 
15.21. Within
the context of a multiple-regression equation, we cannot look at one variable
alone. The slope for one variable is only the slope for that variable when all
other variables are held constant. The
percentage of mothers not seeking care until the third trimester is correlated
with a number of other variables.
1. Observations
can fall within normal ranges on each individual variable and still be outliers
on a bivariate distribution. This is
because an observation may not be normal when paired with the observation on
another variable (it may be unusual to have that combination), e.g., it would
not be unusual to find someone who is 6’2 (height) or to find someone who
weighs 100 pounds. However, it would be
unusual for these two things to be found in the same person. Thus, an observation may be normal on one
variable’s distribution and an outlier in a plot of two variables.
2. Semi-partial
and partial correlations are terms used with multiple linear regression. Semipartial correlation refers to the amount
of variation that a model explains that is accounted for out of the total
variation by a single predictor. Partial
correlation refers to the amount of unexplained variation that is accounted for
by including a particular predictor in the model.
3(a). Partial correlation=
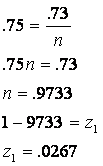
The
first predictor accounts for only 2.67% of the variation of the criterion (
), which indicates it is not likely to be a significant
predictor of the criterion. The second
variable accounts for 73% of the variation in the criterion (
), which indicates it likely is a significant predictor of
the criterion.
3(b). Partial=
partial=
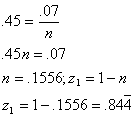
The
first variable accounts for 84.4% (
)of the variation of the criterion, indicating it is likely
to be a significant predictor in the regression model. The second variable accounts for only 7% (
)of the variation in the criterion, indicating it is not
likely to be a significant predictor in the regression model.
4. The
three classes of diagnostic statistics are distance, leverage, and influence.
Distance statistics measure the distance between a point and the regression
line (e.g., residual) and they allow for the identification of outliers. Leverage statistics are those that measure
the degree to which a point in unusual with respect to the predictor variable
(e.g., SD) and allows for the determination of outliers. Influence statistics determine the amount of
influence a point or potential outlier has on a regression line (by taking the
distance and leverage of a point into this determination as well).
5. Unexplained variation=.218
1-.218=.782
explained variation (of the model)
1-
unexplained variation with just 
in the
model=1-.542=.458
partial
correlation=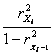
partial
correlation=
Collinearity=.340-.240=.1