PSY 555 Homework 14

Answers

Chapter 9: #10,11,13,14,15,16,18

9.10

Y=.0689X + 3.5306 is the regression equation.

9.11

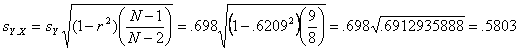
The standard error of the estimate for the regression equation, Y=.0689X + 3.5306, is .5803.

9.13. X=70

Y=.0689X + 3.5306

Y=.0689(70) + 3.5306

Y=8.3536

The predicted incidence of babies with birth weights less than 2500 grams, if the fertility rate rises to 70, would be 8.36.

9.14. The values of X that have been examined in the present study fall between 38 and 56, so the regression equation is based on values within this range. Because we did not examine X values other than those within this range (i.e., fertility rates around 70) and include such values when calculating the regression equation, we cannot be sure what the data does at values around 70 or that the regression equation (if recalculated to include values such as 70) would even be the same. Therefore, we should not be confident making a prediction about the incidence of low birthweight babies if the fertility rate was 70 because we would be extrapolating way beyond the range of the data on which the equation is based.

9.15. X=8

N=107

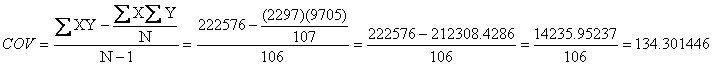
The prediction number of symptoms for an individual with a stress score of 8 would be 80.2.

9.16.

The predicted value of Y when would be 90.704, which is essentially equal to the mean of Y (). This makes sense because the predicted value of Y, given the mean value of X, will be the average value of Y (since that will be a point on the regression line since the line is based on information) involving the means of X and Y).

9.18. .9X+15=1.5X+10

-9X -10 -.9X-10

5=.6X

X=8.3

The equations allow us to determine that at 8.33 years faculty and administrators have equal salaries, but after 8.33 years, the administrators make higher salaries (faculty make more before 8.33 years and they will become equal in salary at approximately 8.33 years of service). The regression equation for faculty shows that the best estimate of starting salary for faculty is $15,000 (the intercept in the equation). For every additional year of service, salary increases on average by $900 (the slope). For administrative staff, the best estimate of starting salary is $10,000 (the intercept), but every year of additional service increases the salary by an average of $1500 (the slope).

1. R-squared (r) is also known as the coefficient of determination. R allows you to determine the amount of variation in the criterion variable that can be explained by the predictor variable. The amount of variation that the predictor variable accounts for is obviously an indicator of how strong a predictor that variable is. However, it is important to note that r does not indicate a causal link between the predictor and the criterion variables. Yet, r may provide more information as to whether the predictor variable is a strong predictor and, if so, how strong a predictor it is. R may also allow you to determine which variables are best suited to be included in a model (or, at least, the adjusted r value can).

2. The pros of such a study include the fact that the high positive correlation (r=.80) between BAC and accidents indicates the two variables are strongly related and supports the researcher’s hypothesis. The N is rather large, which is a pro. Additionally, the r is .64, so 64% of the variation in accidents can be explained by blood alcohol content. However, the main con about the apparent goal of this study is that the researcher is trying to establish a causal link on the basis of a correlational study (and correlation does not equal causation). Therefore, the researcher, while clearly demonstrating a strong relation between alcohol and accidents, cannot conclude that alcohol causes accidents, despite the large correlation.