PSY 555 Homework 11
Answers
Chapter 7: #6,8,9,10,13,14,16,25 (for each problem involving t-tests,
please list what type of test is appropriate to be used).
7.6(a). ![]()
z=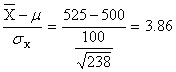
The
probability of a z as extreme as ![]() , so we would reject the hypothesis that the SAT has a mean
of 500 and a standard deviation of 100.
, so we would reject the hypothesis that the SAT has a mean
of 500 and a standard deviation of 100.
7.6(b). Using
a one-tailed (![]() ), the null hypothesis would not have been rejected because
the difference (although significant by a two-tailed test), was in the
unexpected direction.
), the null hypothesis would not have been rejected because
the difference (although significant by a two-tailed test), was in the
unexpected direction.
7.8.
z=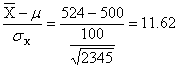
We
would reject H0.
7.9. The
answer to Exercise 7.8 differs substantially from Exercise 7.6 because the sample
sizes are so very different. I
deliberately sought examples where the means were nearly the same, but with
that large difference in sample size, so the resulting z values, and associated
probabilities, are very different.
7.10. For the
CI.95=![]() =525
=525![]()
![]()
![]() =525
=525![]()
512.3![]()
The
95% confidence interval would be 512.3 to 537.7.
7.13(a). Performance
when not reading passage
t=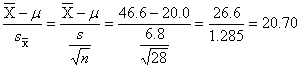
7.13(b). This
does not mean that the SAT is not a valid measure, but it does show that people
who do well at guessing answers also do well on the SAT. This is not very surprising.
7.14(a)
Testing
the experimental hypothesis that children tend to give socially-approved
responses:
I
would compare the mean of this group to the mean of a population of children
tested under normal conditions.
7.14(b). The
null hypothesis would be that these children come from a population with a mean
of 3.87 (the mean of children in general).
The research hypothesis would be that these children give
socially-approved responses at a different rate from normal children because of
the stress they are under.
7.16. Beta-endorphin levels:
Gain
scores:
10
7.5 5.5 6 9.5 -2.5 13 3 -.1 .2 20.3 4 8 25 7.2 35 -3.5 -1.9 .1
Mean=7.70
SD=9.945
t=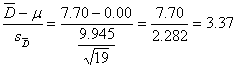
Reject
H0 and conclude that beta-endorphin levels were higher just before
surgery.
7.25(a). Everitt's Family Therapy Group:
We
want to test the null hypothesis that the mean weight was the same before and
after treatment.
t=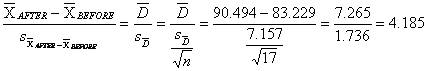
7.25(b). t=4.185 on 16 df, which
tells us that there was a significant gain in weight over the course of
therapy.
1. Within
subjects t-tests are used when the same participants are present in both groups
being compared (i.e., a pre and post group, different drug conditions, etc.). Between
subjects t-tests are used when different participants comprise the groups being
compared (i.e., gender comparisons, most t-tests where you are looking for
differences on a given categorical variable). The types of within subjects t–tests include difference score t-tests, matched
sample t-tests, related sample t-tests, and repeated measures tests. Between subjects t-test refer to those that
are conducted on two independent samples.
2. We
need to test for homogeneity of variance because it is an assumption of the
t-statistic. If heterogeneity of
variance exists, then the values in the t-distribution table will not
accurately reflect the probability of occurrence in your sample. If heterogeneity of variance exists, we need
to make a correction to the degrees of freedom to ensure that our conclusions
are sound.